Teachable Moments | March 7, 2024
A Prime Year for NASA's Pi Day Challenge
Learn how pi is used by NASA and how many of its infinite digits have been calculated, then explore the science and engineering behind the 2024 Pi Day Challenge.
Update: March 15, 2024 – The answers to the 2024 NASA Pi Day Challenge are here! Take a peek at the illustrated answer key now available under each problem on the NASA Pi Day Challenge page.
This year marks the 11th installment of the NASA Pi Day Challenge. Celebrated on March 14, Pi Day is the annual holiday that pays tribute to the mathematical constant pi – the number that results from dividing any circle's circumference by its diameter.
Every year on March 14, Pi Day gives us a reason to enjoy our favorite sweet and savory pies and celebrate the mathematical wonder that helps NASA explore the universe. Students can join in the fun once again by using pi to explore Earth and space themselves with the NASA Pi Day Challenge.
Read on to learn more about the science behind this year's challenge and get students solving real problems faced by NASA scientists and engineers exploring Earth, the Moon, asteroids, and beyond!

Visit the Pi in the Sky 11 lesson page to explore classroom resources and downloads for the 2024 NASA Pi Day Challenge. Image credit: NASA/JPL-Caltech | + Expand image
What is Pi
Dividing any circle’s circumference by its diameter gives you an answer of pi, which is usually rounded to 3.14. Because pi is an irrational number, its decimal representation goes on forever and never repeats. In 2022, mathematician Simon Plouffe discovered the formula to calculate any single digit of pi. In the same year, teams around the world used cloud computing technology to calculate pi to 100 trillion digits. But you might be surprised to learn that for space exploration, NASA uses far fewer digits of pi.
Here at NASA, we use pi to map the Moon, measure Earth’s changing surface, receive laser-coded messages from deep space, and calculate asteroid orbits. But pi isn’t just used for exploring the cosmos. Since pi can be used to find the area or circumference of round objects and the volume or surface area of shapes like cylinders, cones, and spheres, it is useful in all sorts of ways. Transportation teams use pi when determining the size of new subway tunnels. Electricians can use pi when calculating the current or voltage passing through circuits. And you might even use pi to figure out how much fencing is needed around a circular school garden bed.
In the United States, March 14 can be written as 3.14, which is why that date was chosen for celebrating all things pi. In 2009, the U.S. House of Representatives passed a resolution officially designating March 14 as Pi Day and encouraging teachers and students to celebrate the day with activities that teach students about pi. And that's precisely what the NASA Pi Day Challenge is all about!
The Science Behind the 2024 NASA Pi Day Challenge
This 11th installment of the NASA Pi Day Challenge includes four illustrated math problems designed to get students thinking like scientists and engineers to calculate how to get a laser message to Earth, the change in an asteroid’s orbit, the amount of data that can be collected by an Earth satellite, and how a team of mini rovers will map portions of the Moon’s surface.
Read on to learn more about the science and engineering behind each problem or click the link below to jump right into the challenge.
› Take the NASA Pi Day Challenge
› Educators, get the lesson here!
Receiver Riddle
In December 2023, NASA tested a new way to communicate with distant spacecraft using technology called Deep Space Optical Communications, or DSOC. From 19,000,000 miles (30,199,000 km) away, the Psyche spacecraft beamed a high-definition video encoded in a near-infrared laser to Earth. The video, showing a cat named Taters chasing a laser, traveled at the speed of light, where it was received at Caltech’s Palomar Observatory. Because of the great distance the laser had to travel, the team needed to aim the transmission at where Earth would be when the signal arrived. In Receiver Riddle, use pi to determine where along Earth's orbit the team needed to aim the laser so that it could be received at the Observatory at the correct moment.
This animation shows how DSOC's laser signals are sent between the Psyche spacecraft and ground stations on Earth - first as a pointing reference to ensure accurate aiming of the narrow laser signal and then as a data transmission to the receiving station. Credit: NASA/JPL-Caltech/ASU| Watch on YouTube
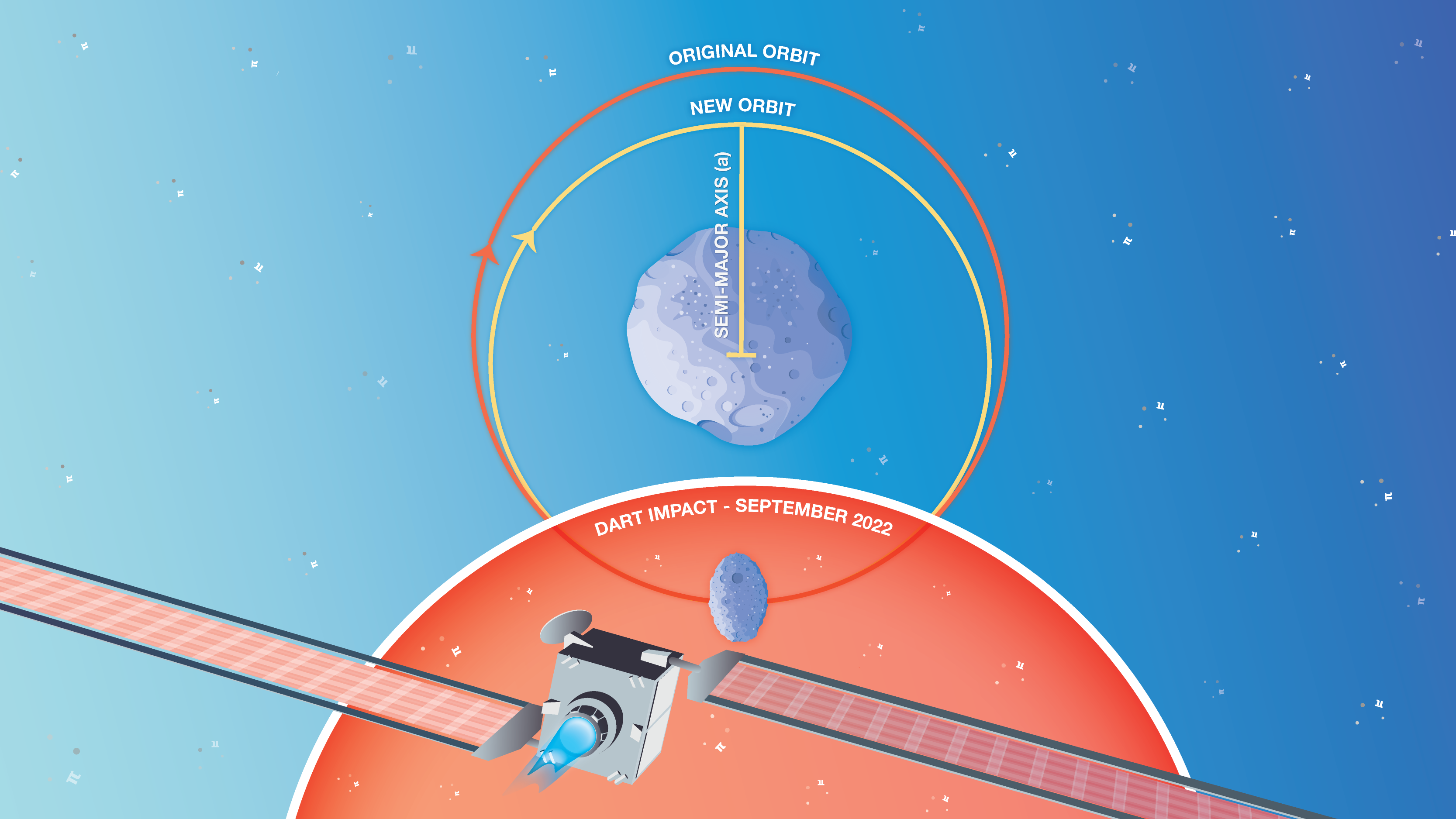
Daring Deflection
In 2022, NASA crashed a spacecraft into the asteroid Dimorphos in an attempt to alter its orbit. The mission, known as the Double Asteroid Redirection Test, or DART, took place at an asteroid that posed no threat to our planet. Rather, it was an ideal target for NASA to test an important element of its planetary defense plan. DART was designed as a kinetic impactor, meaning it transferred its momentum and kinetic energy to Dimorphos upon impact, altering the asteroid's orbit. In Daring Deflection, use pi to determine the shape of Dimorphos’ orbit after DART crashed into it.

This image shows the final minutes of images leading up to the DART spacecraft's intentional collision with asteroid Dimorphos. Credit: NASA/Johns Hopkins APL | › Enlarge image
Orbit Observation
The NISAR mission is an Earth orbiting satellite designed to study our planet's changing ecosystems. It will collect data about Earth's land- and ice-covered surfaces approximately every 6 days, allowing scientists to study changes at the centimeter scale – an unprecedented level of detail. To achieve this feat, NISAR will collect massive amounts of data. In Orbit Observation, students use pi to calculate how much data the NISAR spacecraft captures during each orbit of Earth.

The NISAR satellite, shown in this artist’s concept, will use advanced radar imaging to provide an unprecedented view of changes to Earth’s land- and ice-covered surfaces. Credit: NASA/JPL-Caltech. | › Full image and caption
Moon Mappers
The CADRE project aims to land a team of mini rovers on the Moon in 2025 as a test of new exploration technology. Three suitcase-size rovers, each working mostly autonomously, will communicate with each other and a base station on their lunar lander to simultaneously measure data from different locations. If successful, the project could open the door for future multi-robot exploration missions. In Moon Mappers, students explore the Moon with pi by determining how far a CADRE rover drives on the Moon’s surface.

Engineers test the system that will lower three small rovers onto the lunar surface as part of the CADRE project. Credit: NASA/JPL-Caltech | › Full image and caption
Bring the Challenge Into the Classroom
Celebrate Pi Day by getting students thinking like NASA scientists and engineers to solve real-world problems in the NASA Pi Day Challenge. In addition to solving the 2024 challenge, you can also dig into the 40 puzzlers from previous challenges available in our Pi Day collection. Completing the problem set and reading about other ways NASA uses pi is a great way for students to see the importance of the M in STEM.
-
 Collection
CollectionEducator Guides – NASA Pi Day Challenge
Here's everything you need to bring the NASA Pi Day Challenge into the classroom.
Grades 4-12
Time Varies
-
 Student Activity
Student ActivityNASA Pi Day Challenge
The entire NASA Pi Day Challenge collection can be found in one, handy collection for students.
Grades 4-12
Time Varies
-

Downloads
Can't get enough pi? Download this year's NASA Pi Day Challenge graphics, including mobile phone and desktop backgrounds:
More Pi Resources
-
 Article
ArticleHow Many Decimals of Pi Do We Really Need?
While you may have memorized more than 70,000 digits of pi, world record holders, a JPL engineer explains why you really only need a tiny fraction of that for most calculations.
-
 Article
Article18 Ways NASA Uses Pi
Whether it's sending spacecraft to other planets, driving rovers on Mars, finding out what planets are made of or how deep alien oceans are, pi takes us far at NASA. Find out how pi helps us explore space.
- Article
10 Ways to Celebrate Pi Day With NASA on March 14
Find out what makes pi so special, how it’s used to explore space, and how you can join the celebration with resources from NASA.
-
 Infographic
InfographicPlanet Pi
This poster shows some of the ways NASA scientists and engineers use the mathematical constant pi (3.14) and includes common pi formulas.
-
 Article
Article18 Maneras en Que la NASA Usa Pi
Pi nos lleva lejos en la NASA. Estas son solo algunas de las formas en que pi nos ayuda a explorar el espacio.
Related Lessons for Educators
-
 Lesson
LessonCollisions in Space
Students predict and observe what happens when two objects collide to model collisions in space.
Grades K-4
Time 30 min to 1 hour
-
 Lesson
LessonMoon Phases
Students learn about the phases of the moon by acting them out.
Grades 1-6
Time 30 min to 1 hour
-
 Lesson
LessonModeling an Asteroid
Lead a discussion about asteroids and their physical properties, then have students mold their own asteroids out of clay.
Grades 3-5
Time 30 min to 1 hour
-
 Lesson
LessonMath Rocks: A Lesson in Asteroid Dynamics
Students use math to investigate a real-life asteroid impact.
Grades 8-12
Time 30 min to 1 hour
-
 Lesson
LessonModeling Crustal Folds
Students use playdough to model how Earth’s crust is bent and folded by tectonic plates over geologic time.
Grades 6-12
Time 30 min to 1 hour
-
 Lesson
LessonMaking Topographic Maps
Students draw and interpret topographic maps while learning about technology used to map Earth's surface, the seafloor, and other worlds.
Grades 6-12
Time 30 min to 1 hour
-
 Lesson
LessonCode a Radio Message for Space
Students code microcontrollers to send and receive radio signals, simulating communications between Earth and spacecraft.
Grades 6-12
Time 30 min to 1 hour
Related Activities for Students
-
 Student Project
Student ProjectDraw Your Own Psyche Spacecraft
Follow these easy instructions to draw and decorate your own model of the Psyche spacecraft.
Type Project
Subject Engineering
-
 Slideshow
SlideshowWhat's That Space Rock?
Find out how to tell the difference between asteroids, comets, meteors, meteorites and other bodies in our solar system.
Type Slideshow
Subject Science
Facts and Figures
Websites
Articles
- How NASA Studies and Tracks Asteroids Near and Far
- NASA Cat Video Explained
- Article for Kids: Asteroid or Meteor: What's the Difference?
- Article for Kids: What Is an Asteroid?
Videos
- The Video NASA’s Laser Communications Experiment Streamed From Deep Space
- NASA's DART Mission Confirms Crashing Spacecraft into Asteroids Can Deflect Them
Interactives
TAGS: Pi Day, Pi, Math, NASA Pi Day Challenge, moon, earth, asteroid, psyche, DART, CADRE, NISAR DSOC
Edu News | January 16, 2024
Doing the Math on Why We Have Leap Day
Leap day, Feb. 29, happens every four years because of a mismatch between the calendar year and Earth's orbit. Learn how it works, and get students engaged in leap day STEM.
You may have noticed that there's an extra day on your calendar this year. That's not a typo – it's leap day! Leap day is another name for Feb. 29, a date that typically comes around every four years, during a leap year.
Why doesn't Feb. 29 appear on the calendar every year?
The length of a year is based on how long it takes a planet to revolve around the Sun. Earth takes about 365.2422 days to make one revolution around the Sun. That's about six hours longer than the 365 days that we typically include in a calendar year. As a result, every four years, we have about 24 extra hours that we add to the calendar at the end of February in the form of leap day.
Without leap day, the dates of annual events, such as equinoxes and solstices, would slowly shift to later in the year, changing the dates of each season. After only a century without leap day, summer wouldn’t start until mid-July!
But the peculiar adjustments don't end there. If Earth revolved around the Sun in exactly 365 days and six hours, this system of adding a leap day every four years would need no exceptions. However, Earth takes a little less time than that to orbit the Sun. Rounding up and inserting a 24-hour leap day every four years adds about 45 extra minutes to every four-year leap cycle. That adds up to about three days every 400 years. To correct for that, years that are divisible by 100 don't have leap days unless they’re also divisible by 400.
If you do the math, you'll see that the year 2000 was a leap year, but 2100, 2200 and 2300 will not be.
Have students learn more about leap years with this article from NASA's Space Place, then have them do the math for themselves with this leap day problem set. You can also have students write a letter or poem to be opened on the next leap day or get them learning about orbits across the solar system.
And since we've got an extra 24 hours this year, don't forget to take a little time to relax!
Educator Resources
-
 Problem Set
Problem SetLeap Day Math
In this problem set, students calculate the difference between the calendar year and Earth's orbital period to determine when leap years occur.
Subject Math
Grades 5-8
Time Less than 30 mins
-
 Collection
CollectionSolar System Scale & Size Lessons
Explore a collection of standards-aligned lessons all about the size and scale of our solar system.
-
 Educator Guide
Educator GuidePlanetary Poetry
Have students write a poem they can open and re-read next leap day!
Subject Science
Grades 2-12
Time 1-2 hrs
Student Resources
-
 Article
ArticleWhat Is a Leap Year?
Get the answer in this article from NASA Space Place. Plus, learn if other planets have leap years!
-
 Article
ArticleHow Long Is a Year on Other Planets?
Get the answer in this article from NASA Space Place.
-
 Collection
CollectionAll About the Size and Scale of the Solar System
Learn how big and far away the planets are with these projects and activities.
TAGS: K-12 Education, Math, Leap Day, Leap Year, Events, Space, Educators, Teachers, Parents, Students, STEM, Lessons, Earth Science, Earth
Teacher Feature | April 3, 2023
Working With the Next Wave of Science Teachers
Four pre-service teachers at Cal Poly Pomona are developing their skills in lesson design and delivery as they study Earth science concepts and prepare for graduation.

Clockwise from upper left: Amie Gallardo, Sofia Vallejo, Afiya Kindle, Jacquelin Galvez-Coyt. Image courtesy: Brandon Rodriguez | + Expand image
During the fall semester of 2022, I had the privilege of working with the Education Department at California Polytechnic University in Pomona, specifically with pre-service teachers taking coursework in Earth science. During our collaboration, the curriculum had the students split time in class between learning about geology and Earth’s history and then designing and engaging in classroom activities related to the technical content that they could take to their own classes in the future. This combination had Cal Poly students learning science and education hand-in-hand each week and led to some amazing classroom lessons and lab activities.
One group of young women in the program stood out as exceptionally passionate about their future careers. This team consisted of four seniors: Jacquelin Galvez-Coyt, hoping to someday teach kindergarten; Amie Gallardo, who is planning to teach fourth grade; Afiya Kindle, who is interested in teaching elementary or middle school; and Sofia Vallejo, who is interested in kindergarten through sixth grade.
Despite their interest in working with young students and collaborating to design lessons for those students, each of these pre-service teachers allowed their individuality to shape how they navigated lesson design and implementation. I recently sat down with them to ask about their instructional style and aspirations for classrooms of their own.
Now that we’re back to in-person classes, how is the transition going?
Sofia: Returning from remote instruction felt eerie at first, but it’s so nice to return to communicate with people and build connections in a non-digital way. In-person classes prepare you to communicate with colleagues in real life, build social skills, and read body language. All of these skills are critical for a teacher in order to understand and better help students to succeed.
Amie: Returning from remote instruction has been amazing. While it had its perks, I believe, as students, we learn a lot more while working hands-on with our projects than is possible in distance learning. If we’re trying to develop and assess activities we can do with kids, that really requires being face-to-face.

Amie Gallardo provides an Earth science demonstration to a class of education students at Cal Poly Pomona. Image courtesy: Brandon Rodriguez | + Expand image
What are you most excited about when it comes to having your own classroom, and how will you get your kids excited about STEM?
Afiya: I am most confident about creating a genuine safe space for kids. I’ll be able to communicate how much I care about them and about our shared future, and I think there could never be enough genuinely kind and caring teachers in this world.
Jacquelin: I think my kids will be excited about STEM because of how easy it's become to incorporate activities. There are many resources out there for teachers to use for teaching math and science that don't rely solely on a textbook. Activities that use inexpensive materials or that require a little DIY skills go a long way for students.
Afiya: Exactly! I know I developed my love for science from being hands-on and actually somewhat “in charge” of an experiment on my own. Winning a science fair competition in seventh grade for a greenhouse I built really boosted my confidence and helped reassure me of my scholastic abilities as a kid.
You led a really cool lesson with your classmates where you had them use Oreos to model tectonic boundaries. How do you feel that lesson went?
Jacqueline: I was really proud of our group. After giving a lecture to the students about tectonic plate boundaries, we dispersed Oreos to everyone. We were set up around the classroom demonstrating the activity and giving verbal instructions for everyone to follow. My favorite part was when I saw two students by me go, “Oohhhh,” and smile once they got their Oreos to demonstrate the plate boundaries correctly.
Amie: I thought it went really well! All the students in our classroom enjoyed it. Although we, as adults, may know about plate tectonics, having our hands on the Oreos to understand it made it more enjoyable.
Afiya: Plus, who doesn’t love Oreos? They’re even vegan!

An Oreo cookie is used to demonstrate rock fault movement. Image courtesy: Brandon Rodriguez | + Expand image
Which of the NASA-JPL lessons that you’ve implemented did you enjoy, and why?
Jacqueline: My favorite JPL activity we did was the Moon Phases activity. Having one team member to the side to give the instructions allows another student to view the different Moon phases. Then you switch so both students get to see that perspective. My second favorite activity was creating layers with different colored Play-Doh and demonstrating them as different plate boundaries and folds.
Amie: The NASA lesson that I enjoyed the most was the one we did on lunar eclipses. Much like myself, many students often have an early fascination with the Moon. Learning more about the Moon and lunar eclipses made me excited about the semester.

Sofia Vallejo uses a foam ball and lamp to demonstrate how solar eclipses occur. Image courtesy: Brandon Rodriguez | + Expand image
What’s next for you after you finish at Cal Poly Pomona?
Jacqueline: After I graduate at Cal Poly, I plan to attend UC Riverside to complete my credential program. While I am there, I would love to get my student teaching experience. Once I complete my credential program, I plan to apply to work at schools in the Inland Empire [in Southern California]. I want to be able to give back to the communities that influenced who I am today.
Sofia: My plans after Cal Poly are to take some time off to gain experience in the field as a substitute teacher. I also am looking to gain more volunteer experience, skills, and exposure. In the future, I want to enroll in UC Riverside to earn my teaching credential and master's degree.
Looking for ways to bring NASA STEM into your classroom or already have a great idea? The Education Office at NASA's Jet Propulsion Laboratory serves educators in the greater Los Angeles area. Contact us at education@jpl.nasa.gov.
Explore More
TAGS: Teachers, School, Remote School, Classroom, Instruction, K-12, STEAM, Science, Math, resources, lessons
Teachable Moments | March 9, 2023
10 Years of NASA's Pi Day Challenge
Learn how pi is used by NASA and how many of its infinite digits have been calculated, then explore the science and engineering that makes the Pi Day Challenge possible.
Update: March 15, 2023 – The answers are here! Visit the NASA Pi Day Challenge page to view the illustrated answer keys for each problem.
This year marks the 10th installment of the NASA Pi Day Challenge. Celebrated on March 14, Pi Day is the annual holiday that pays tribute to the mathematical constant pi – the number that results from dividing any circle's circumference by its diameter.
Every year, Pi Day gives us a reason to celebrate the mathematical wonder that helps NASA explore the universe and enjoy our favorite sweet and savory pies. Students can join in the fun once again by using pi to explore Earth and space themselves in the NASA Pi Day Challenge.
Read on to learn more about the science behind this year's challenge and find out how students can put their math mettle to the test to solve real problems faced by NASA scientists and engineers as we explore Earth, Mars, asteroids, and beyond!

Visit the Pi in the Sky 10 lesson page to explore classroom resources and downloads for the 2023 NASA Pi Day Challenge. Image credit: NASA/JPL-Caltech | + Expand image

This illustration shows a concept for multiple robots that would team up to ferry to Earth samples of rocks and soil being collected from the Martian surface by NASA's Mars Perseverance rover. Image credit: NASA/JPL-Caltech | › Full image and caption

Image from animation comparing the relative sizes of James Webb's primary mirror to Hubble's primary mirror. Credit: NASA/Goddard Space Flight Center . | › Full animation

This illustration depicts the metal-rich asteroid Psyche, which is located in the main asteroid belt between Mars and Jupiter. Credits: NASA/JPL-Caltech/ASU | + Full image and caption

This image sequence shows an annular solar eclipse from May 2012. The bottom right frame illustrates the distinctive ring, or "annulus," of such eclipses. A similar eclipse will be visible from the South Pacific on May 10, 2013. Credits: Brocken Inaglory, CC BY-SA 3.0, via Wikimedia Commons | + Expand image
How It Works
Dividing any circle’s circumference by its diameter gives you an answer of pi, which is usually rounded to 3.14. Because pi is an irrational number, its decimal representation goes on forever and never repeats. In 2022, mathematician Simon Plouffe discovered the formula to calculate any single digit of pi. In the same year, teams around the world used cloud computing technology to calculate pi to 100 trillion digits. But you might be surprised to learn that for space exploration, NASA uses far fewer digits of pi.
Here at NASA, we use pi to measure the area of telescope mirrors, determine the composition of asteroids, and calculate the volume of rock samples. But pi isn’t just used for exploring the cosmos. Since pi can be used to find the area or circumference of round objects and the volume or surface area of shapes like cylinders, cones, and spheres, it is useful in all sorts of ways. Transportation teams use pi when determining the size of new subway tunnels. Electricians can use pi when calculating the current or voltage passing through circuits. And you might even use pi to figure out how much fencing is needed around a circular school garden bed.
In the United States, March 14 can be written as 3.14, which is why that date was chosen for celebrating all things pi. In 2009, the U.S. House of Representatives passed a resolution officially designating March 14 as Pi Day and encouraging teachers and students to celebrate the day with activities that teach students about pi. And that's precisely what the NASA Pi Day Challenge is all about!
The Science Behind the 2023 NASA Pi Day Challenge
This 10th installment of the NASA Pi Day Challenge includes four noodle-nudgers that get students using pi to calculate the amount of rock sampled by the Perseverance Mars rover, the light-collecting power of the James Webb Space Telescope, the composition of asteroid (16) Psyche, and the type of solar eclipse we can expect in October.
Read on to learn more about the science and engineering behind each problem or click the link below to jump right into the challenge.
› Take the NASA Pi Day Challenge
› Educators, get the lesson here!
Tubular Tally
NASA’s Mars rover, Perseverance, was designed to collect rock samples that will eventually be brought to Earth by a future mission. Sending objects from Mars to Earth is very difficult and something we've never done before. To keep the rock cores pristine on the journey to Earth, the rover hermetically seals them inside a specially designed sample tube. Once the samples are brought to Earth, scientists will be able to study them more closely with equipment that is too large to make the trip to Mars. In Tubular Tally, students use pi to determine the volume of a rock sample collected in a single tube.
Rad Reflection
When NASA launched the Hubble Space Telescope in 1990, scientists hoped that the telescope, with its large mirror and sensitivity to ultraviolet, visible, and near-infrared light, would unlock secrets of the universe from an orbit high above the atmosphere. Indeed, their hope became reality. Hubble’s discoveries, which are made possible in part by its mirror, rewrote astronomy textbooks. In 2022, the next great observatory, the James Webb Space Telescope, began exploring the infrared universe with an even larger mirror from a location beyond the orbit of the Moon. In Rad Reflection, students use pi to gain a new understanding of our ability to peer deep into the cosmos by comparing the area of Hubble’s primary mirror with the one on Webb.
Metal Math
Orbiting the Sun between Mars and Jupiter, the asteroid (16) Psyche is of particular interest to scientists because its surface may be metallic. Earth and other terrestrial planets have metal cores, but they are buried deep inside the planets, so they are difficult to study. By sending a spacecraft to study Psyche up close, scientists hope to learn more about terrestrial planet cores and our solar system’s history. That's where NASA's Psyche comes in. The mission will use specialized tools to study Psyche's composition from orbit. Determining how much metal exists on the asteroid is one of the key objectives of the mission. In Metal Math, students will do their own investigation of the asteroid's makeup, using pi to calculate the approximate density of Psyche and compare that to the density of known terrestrial materials.
Eclipsing Enigma
On Oct. 14, 2023, a solar eclipse will be visible across North and South America, as the Moon passes between Earth and the Sun, blocking the Sun's light from our perspective. Because Earth’s orbit around the Sun and the Moon’s orbit around Earth are not perfect circles, the distances between them change throughout their orbits. Depending on those distances, the Sun's disk area might be fully or only partially blocked during a solar eclipse. In Eclipsing Enigma, students get a sneak peek at what to expect in October by using pi to determine how much of the Sun’s disk will be eclipsed by the Moon and whether to expect a total or annular eclipse.
Teach It
Celebrate Pi Day by getting students thinking like NASA scientists and engineers to solve real-world problems in the NASA Pi Day Challenge. In addition to solving this year’s challenge, you can also dig into the more than 30 puzzlers from previous challenges available in our Pi Day collection. Completing the problem set and reading about other ways NASA uses pi is a great way for students to see the importance of the M in STEM.
Pi Day Resources
-

Pi in the Sky Lessons
Here's everything you need to bring the NASA Pi Day Challenge into the classroom.
Grades 4-12
Time Varies
-

NASA Pi Day Challenge
The entire NASA Pi Day Challenge collection can be found in one, handy slideshow for students.
Grades 4-12
Time Varies
-

How Many Decimals of Pi Do We Really Need?
While you may have memorized more than 70,000 digits of pi, world record holders, a JPL engineer explains why you really only need a tiny fraction of that for most calculations.
-

18 Ways NASA Uses Pi
Whether it's sending spacecraft to other planets, driving rovers on Mars, finding out what planets are made of or how deep alien oceans are, pi takes us far at NASA. Find out how pi helps us explore space.
-
10 Ways to Celebrate Pi Day With NASA on March 14
Find out what makes pi so special, how it’s used to explore space, and how you can join the celebration with resources from NASA.
-

Infographic: Planet Pi
This poster shows some of the ways NASA scientists and engineers use the mathematical constant pi (3.14) and includes common pi formulas.
-

Downloads
Can't get enough pi? Download this year's NASA Pi Day Challenge graphics, including mobile phone and desktop backgrounds:
-

National Council of Teachers of Mathematics: Notice and Wonder
Creative brainstorming through noticing and wondering encourages student participation, engagement, and students' understanding of the NASA Pi Day Challenge.
Subject Mathematics
-
Pi Day: What's Going 'Round
Tell us what you're up to this Pi Day and share your stories and photos on our showcase page.
Plus, join the conversation using the hashtag #NASAPiDayChallenge on Facebook, Twitter, and Instagram.
Related Lessons for Educators
-

Robotic Arm Challenge
In this challenge, students will create a model robotic arm to move items from one location to another. They will engage in the engineering design process to design, build and operate the arm.
Grades K-8
Time 30 min to 1 hour
-

NASA's Mission to Mars Student Challenge
Take part in the exploration of Mars and bring students along for the ride with NASA's Perseverance rover.
Grades K-12
Time Varies
-

Moon Phases
Students learn about the phases of the moon by acting them out.
Grades 1-6
Time 30 min to 1 hour
-

Modeling the Earth-Moon System
Students learn about scale models and distance by creating a classroom-size Earth-Moon system.
Grades 6-8
Time 30 min to 1 hour
-

Math of the Expanding Universe
Students will learn about the expanding universe and the redshift of lightwaves, then perform their own calculations with a distant supernova.
Grades 9-12
Time 30 min to 1 hour
-
The Expanded Universe: Playing with Time Activity Guide
In this activity, participants use balloons to model the expansion of the universe and observe how expansion affects wavelengths of light and distance between galaxies
-

James Webb Space Telescope STEM Toolkit
Find a collection of resources, activities, videos, and more for your students to learn about NASA’s newest space observatory.
-

Modeling an Asteroid
Lead a discussion about asteroids and their physical properties, then have students mold their own asteroids out of clay.
Grades 3-5
Time 30 min to 1 hour
-

Math Rocks: A Lesson in Asteroid Dynamics
Students use math to investigate a real-life asteroid impact.
Grades 8-12
Time 30 min to 1 hour
Related Activities for Students
-

How to Make a Pinhole Camera
Learn how to make your very own pinhole camera to safely see a solar eclipse in action!
Type Project
Subject Engineering
-
Collection: Exploring Mars
Make a cardboard rover, design a Mars exploration video game and explore more STEM projects, slideshows and videos for students.
Type Project
Subject Science
-

What's That Space Rock?
Find out how to tell the difference between asteroids, comets, meteors, meteorites and other bodies in our solar system.
Type Slideshow
Subject Science
-

10 Things We Can Learn from Webb's First Images
Take a closer look at how images from NASA's most powerful space telescope yet are helping to answer some of astronomers' most burning questions.
Type Slideshow
Subject Science
Recursos en español
Facts and Figures
Websites
- Webb Space Telescope
- Mars Exploration
- Perseverance Mars Rover
- Mars Sample Return
- Psyche Mission
- MIRI Instrument
- 2023 Eclipse
Articles
Videos
Interactives
TAGS: Pi Day, Pi, Math, NASA Pi Day Challenge, sun, moon, earth, eclipse, asteroid, psyche, sample return, mars, perseverance, jwst, webb, hubble, telescope, miri
Teacher Feature | May 31, 2022
Math Connections Take Students Far
A Los Angeles math teacher gets students engaged with connections to science and exploring the human side of math, such as how leaders inspire change in their communities.
Katherine Risbrough has been teaching high school math for almost 10 years. She began her teaching career in the Hickory Hill community of Memphis, Tennessee, where she taught everything from Algebra 1 to Calculus and served as a math coach for the district. Five years ago, she came to Los Angeles to teach Integrated Math and Calculus at Synergy Quantum Academy High School.
Outside of math, Ms. Risbrough is also a superfan of college football and never misses a game at her alma mater, the University of Southern California. Her fandom for making the game is rivaled only by her love of Harry Potter, having been to every midnight book and movie release.
I caught up with Ms. Risbrough to find out how she gets students excited about math, and I learned about a new strategy she used this past year: bridging math and science by teaming up with the AP Physics teacher. Her cross-discipline curriculum focused on helping students make connections between subjects and got them engaged as they returned from more than a year of remote learning.
Math can be intimidating for students and it can be difficult to keep them engaged. How do you get your students excited about math?

Ms. Risbrough works with one of her calculus students. Image courtesy: Katherine Risbrough | + Expand image
Sometimes it's easier said than done, but math needs to be as hands-on and discussion-based as possible. We use a lot of the calc-medic curriculum, which is application and discovery first followed by a whole class discussion to share ideas and cement new learning. When students have to speak and defend a hypothesis or an argument, they are practicing mathematical reasoning, which is a skill they can take into all STEM coursework. I avoid lectures as much as possible. We also do a lot of flipped classroom learning (videos at home and practice in class), group work, use technology, and do activities that get students moving around the classroom.
I believe that learning mathematics should be a collaborative, exploratory process and that every student already has the skills necessary to become a successful mathematician. It’s my job to give them opportunities to show off and strengthen those skills, so that they can be just as successful with or without me present to help them.
This year you’ve introduced some interesting projects to make your class more interdisciplinary. Tell me a bit more about that.
I’ve really focused on keeping the math contextualized by being sure the content is interdisciplinary. For example, over half of my AP Calculus students are also taking AP Physics. This year, in particular, I was sure to coordinate with the physics teacher to see how we could align our curriculum in kinematics with what we were doing with integrals and derivatives. This began with students doing JPL’s additive velocity lesson in their physics class to set the stage for how calculus ties together acceleration, velocity, and displacement.
Both classes are so challenging for students, but when they see how strategies in one class can help lift them in another, it’s almost as if they are getting to see two different strategies to solve the same problem. Designing challenges that could be solved with both physics and math gave the students an ability to approach problems from either side. At first, they were pretty intimidated to see their two most challenging classes teaming up, but the end result was some incredible student projects and dramatic improvement in their ability to graph out relationships.
I also kick off new units by making connections to students' own life or even their future careers. They need to know the “why” beyond just, “because you’ll be tested on it.” We try to talk about STEM historical figures and current leaders (specifically mathematicians and scientists of color) as often as possible. For example, I use clips from the movies "October Sky" and "Hidden Figures" to set the stage and then lead into projects about rocket trajectories and elliptical orbits.

Students in Ms. Risbrough's class map out language and processes to better understand shapes and limits in functions. Image courtesy: Katherine Risbrough | + Expand image
This year, in calculus, we started the year with the idea of “Agents of Change” and looked at thought leaders such as veteran astronaut Ellen Ochoa and climate scientist Nicole Hernandez Hammer and how their work relates to “instant rates of change” and “average rates of change” in calculus. Then, I had students think about moments of change in their life, and how that instant can be carried forward to a make a long term change in their careers and communities.
Coming back from COVID-19 and more than a year of remote instruction, how are your students adjusting to being back in the classroom?
Our students missed out on so many social and academic opportunities because of COVID, but they aren’t letting that stop them. The biggest struggle was starting off the school year and getting back into routines. Because of the demographics of our students, there have been more absences than usual, as many of our students help support their family at home. Many parents struggled to keep work through the pandemic, and a lot of my students work outside of school or take care of their siblings. The effects of caring for their families while still trying to focus on applying to college has really taken a toll on students.
I’m fortunate that so many kids are comfortable and open sharing feelings of increased anxiety, responsibility, or worry over the past two years. I believe it's important that my classroom and our group first and foremost be an escape from that space rather than an added stress. Their success in math – even a rigorous AP math class with a breakneck pace – comes from me being there for them as a person first and a teacher second. We focus so much on “catching them up” that we forget to take some time for them to process all they have had to manage.
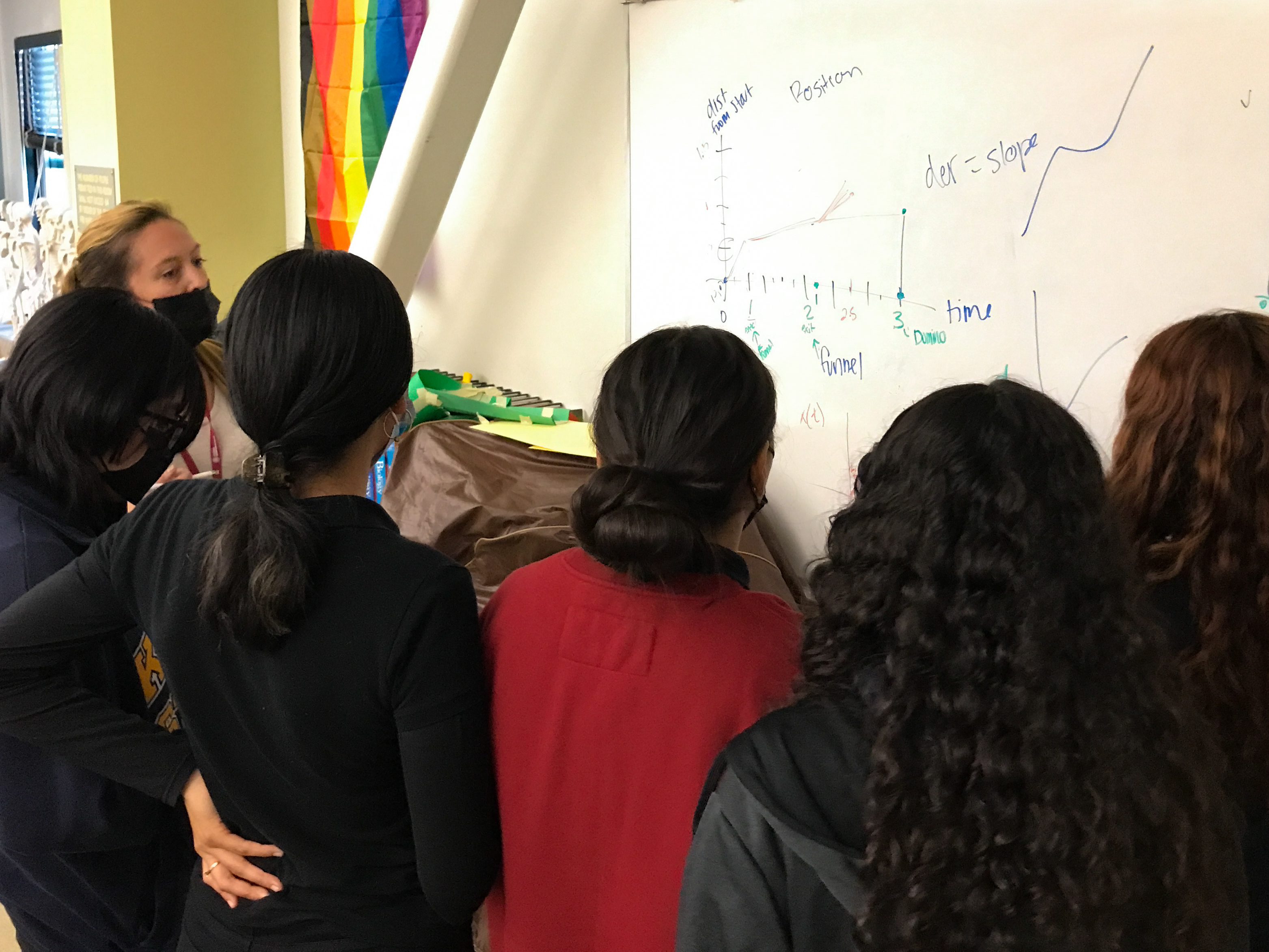
AP Calculus students graph out kinematics as examples of integrals and derivatives. Image courtesy: Katherine Risbrough | + Expand image
As we move toward graduation, what is one story of success that you will take away from this year?
Honestly, it's the success of my students. They have jumped into AP Calculus after 1.5 years of distance learning and the social-emotional learning burdens of Covid, and have done amazing work. They are thoughtful, persistent, and often learning multiple grades worth of skills within one calculus lesson. I guess I'm a small piece of that, but all that I've really done is give them space to explore, discuss, and learn. It's what they've done with that space that has been the best thing to watch!
Looking for ways to bring NASA STEM into your classroom or already have a great idea? The Education Office at NASA's Jet Propulsion Laboratory serves educators in the greater Los Angeles area. Contact us at education@jpl.nasa.gov.
Explore More
-

Ion Propulsion: Using Spreadsheets to Model Additive Velocity
Students develop spreadsheet models that describe the relationship between the mass of a spacecraft, the force acting on the craft, and its acceleration.
Subject Science
Grades 6-12
Time 30-60 mins
-

Math Lessons
Explore a collection of standards-aligned math lessons with links to NASA missions and science.
Subject Math
Grades K-12
Time Varies
TAGS: Teachers, School, Classroom, Instruction, K-12, High School, Math, Calculus, Physics, Algebra, Lessons, Resources
Teacher Feature | April 25, 2022
Back in the Classroom and Getting Creative With STEAM
This fourth-grade teacher is finding creative ways to get her students back into the flow of classroom learning with the help of STEAM education resources from JPL.
Jackie Prosser is a fourth-grade teacher in Fairfield, California, finishing her second year as a classroom teacher. She is a recent graduate of the University of California, Riverside, where she simultaneously received her teaching credential and her master's in education. This was where I was fortunate enough to meet Miss Prosser, through a collaboration between the Education Office at NASA's Jet Propulsion Laboratory and UCR designed to help new teachers incorporate STEM into their future classrooms. She and her cohort immediately struck me as passionate future teachers already exploring unique ways to bring space science into their teaching.
But it's been a challenging transition for Miss Prosser and teachers like her who started their careers amid a pandemic. She began her student-teaching in person only to find that she would have to switch to teaching remotely just four months into the job. Now, she's back in the classroom but facing new challenges getting students up to speed academically while reacquainting them with the social aspects of in-person learning.
I caught up with her to find out how she's managing the transition and developing creative ways to support the individual needs of her students and, at the same time, incorporating science and art into her curriculum with the help of STEAM resources from the JPL Education Office.
What made you want to become an elementary school teacher?
Originally, I became a teacher because I love to see that moment of light when a concept finally clicks in a kid’s mind. I am still a teacher (even after the craziest two years ever) because every kid deserves someone to fight for them, and I know I can be that person for at least 32 kids a year.
I love to teach young kids especially for two reasons. The first is their honesty; no one will tell you exactly like it is like a nine-year-old will. The second is that I love the excitement kids have for learning at this age.
It has been a bumpy couple years, especially this past school year when it was unclear if we would be remote again or back in the classroom. How has it been coming back from remote learning?
Coming back from remote learning has been an incredible challenge, but we’ve come a long way since the beginning of the year. Students really struggled being back in a highly structured environment. It was very hard to balance meeting the individual needs of each student and getting them used to the structure and expectations of the classroom.
My fourth graders were online for the last part of second grade and a vast majority of third grade. This is when students really start to solve conflicts and regulate their emotions with less support from adults. I have seen a lot more problems with emotion regulation and conflict among my students this year than in years past.
There is a lot of pressure on teachers right now to make up for all the learning loss and for students being behind on grade-level standards. But I don’t think enough people talk about how much joy and social interaction they also lost during remote learning. Teachers are also feeling the pressure of that. I want to help my students be the very best versions of themselves and being happy and comfortable with themselves is a huge part of that.

A student looks at a page from the NASA Solar System Exploration website. Image courtesy: Jackie Prosser | + Expand image
How do you structure your class to get students back in the flow of a school setting?
I use a lot of manipulatives in my math lessons and try to make their learning as hands-on as possible. I also teach math in small groups to be able to better meet the individual needs of my students. I have one group with me learning the lesson, one group doing their independent practice of the skill, and one group on their computers. Then, the students switch until each group has done each activity.
You’re a big fan of science and came to several JPL Education workshops while you were still in school yourself. Are there JPL Education resources that you have found particularly impactful for your students?
I have always loved teaching science. It is so often left behind or pushed aside. I think a lot of time that happens because teachers feel like they do not have enough background knowledge to teach high-quality science lessons or they think that the lessons will add to the already enormous workload teachers have. My district does not have an adopted or prescribed curriculum for teachers to follow, so we have a lot of freedom for when and how to make the time for STEAM.
The education resources [from NASA's Jet Propulsion Laboratory] have made it so easy for me to teach and get kids excited about science, and my kids absolutely love them. Our favorites always seem to be Make a Paper Mars Helicopter and Art and the Cosmic Connection.

A student holds a paper Mars helicopter. Image courtesy: Jackie Prosser | + Expand image
I also am part of my district’s science pilot program. It has been so cool to be able to decide what curriculum to pilot and watch my students test it out and give feedback on their learning. Last year, I had the amazing opportunity to teach science for two elementary schools’ summer programs. My partner teacher and I got to create the curriculum for them, and we pulled a ton of lessons from the JPL Education website. It was by far the most fun I have ever had at a job.
Despite being a new teacher, you’ve already seen so much. How have you navigated the changing landscape?
I have an amazing network of teachers supporting me at every turn. My grade-level team and my friends from my credential program are some of the most amazing people and educators I have ever met. There is no way I would be able to get through the more difficult aspects of teaching without them.
I am also coaching the boys soccer team, directing the school’s "Lion King Jr." play, contributing to the science pilot program, and serving on the social committee for teachers and staff. I love using these different roles to make connections with not just my students, but also students from all grades.
Looking for ways to bring NASA STEM into your classroom or already have a great idea? The Education Office at NASA's Jet Propulsion Laboratory serves educators in the greater Los Angeles area. Contact us at education@jpl.nasa.gov.
Explore More
-

Make a Paper Mars Helicopter
In this lesson, students build a paper helicopter, then improve the design and compare and measure performance.
Subject Engineering
Grades 2-8
Time 30-60 mins
-

Art and the Cosmic Connection
Students use art to describe and recognize the geology on planetary surfaces.
Subject Science
Grades K-12
Time 1-2 hrs
TAGS: Teachers, School, Remote School, Classroom, Instruction, K-12, Fourth Grade, STEAM, Science, Math, Art, UC Riverside, resources, lessons
Teachable Moments | March 10, 2022
Pi Goes to Infinity and Beyond in NASA Challenge
Learn about pi and some of the ways the number is used at NASA. Then, dig into the science behind the Pi Day Challenge.
Update: March 15, 2022 – The answers are here! Visit the NASA Pi Day Challenge slideshow to view the illustrated answer keys for each of the problems in the 2022 challenge.
In the News
No matter what Punxsutawney Phil saw on Groundhog Day, a sure sign that spring approaches is Pi Day. Celebrated on March 14, it’s the annual holiday that pays tribute to the mathematical constant pi – the number that results from dividing any circle's circumference by its diameter.
Every year, Pi Day gives us a reason to not only celebrate the mathematical wonder that helps NASA explore the universe, but also to enjoy our favorite sweet and savory pies. Students can join in the fun by using pi to explore Earth and space themselves in our ninth annual NASA Pi Day Challenge.
Read on to learn more about the science behind this year's challenge and find out how students can put their math mettle to the test to solve real problems faced by NASA scientists and engineers as we explore Earth, the Moon, Mars, and beyond!
Visit the Pi in the Sky 9 lesson page to explore classroom resources and downloads for the 2022 NASA Pi Day Challenge. Image credit: NASA/JPL-Caltech | + Expand image

This artist's concept shows the Lunar Flashlight spacecraft, a six-unit CubeSat designed to search for ice on the Moon's surface using special lasers. Image credit: NASA/JPL-Caltech | › Full image details

Clouds drift over the dome-covered seismometer, known as SEIS, belonging to NASA's InSight lander, on Mars. Credit: NASA/JPL-Caltech. | › Full image and caption
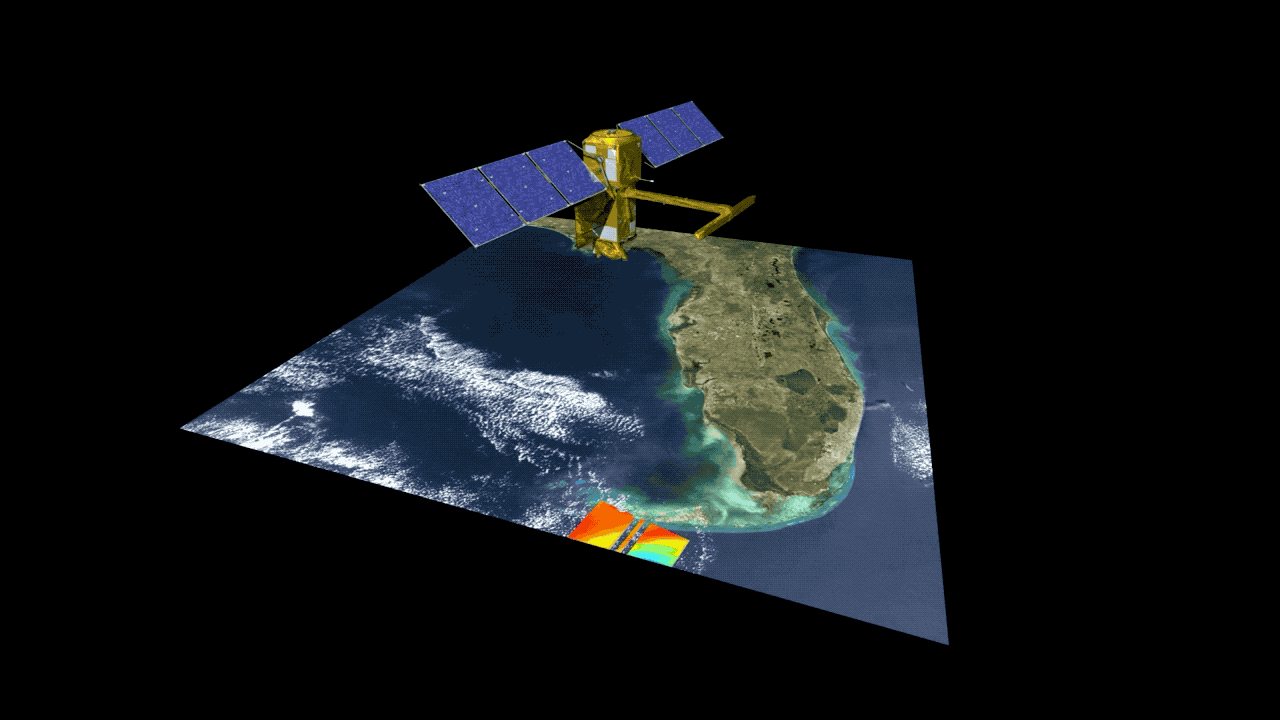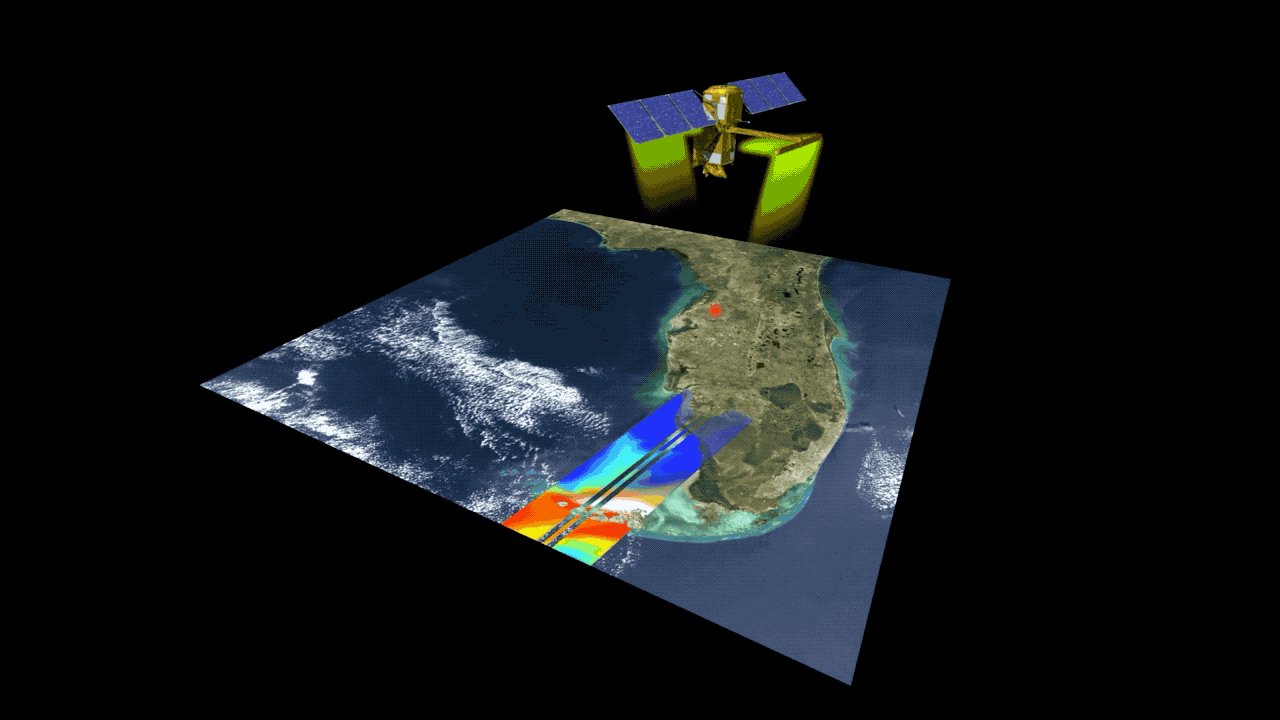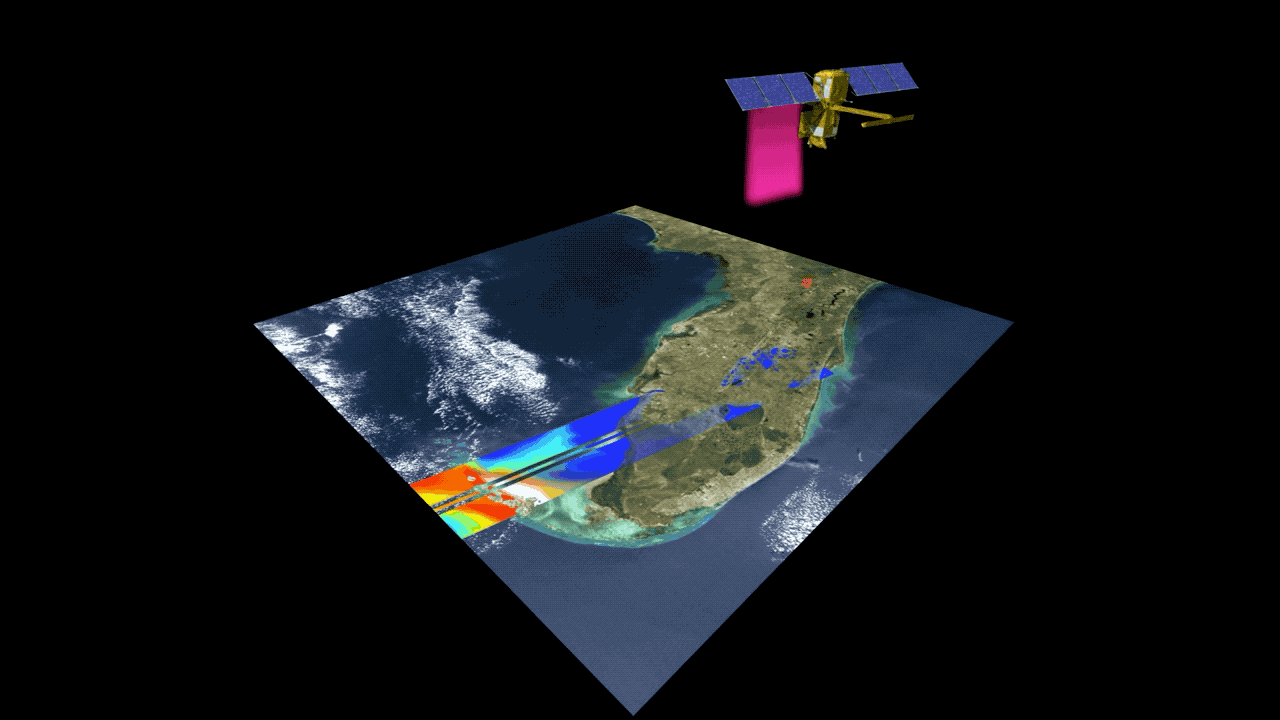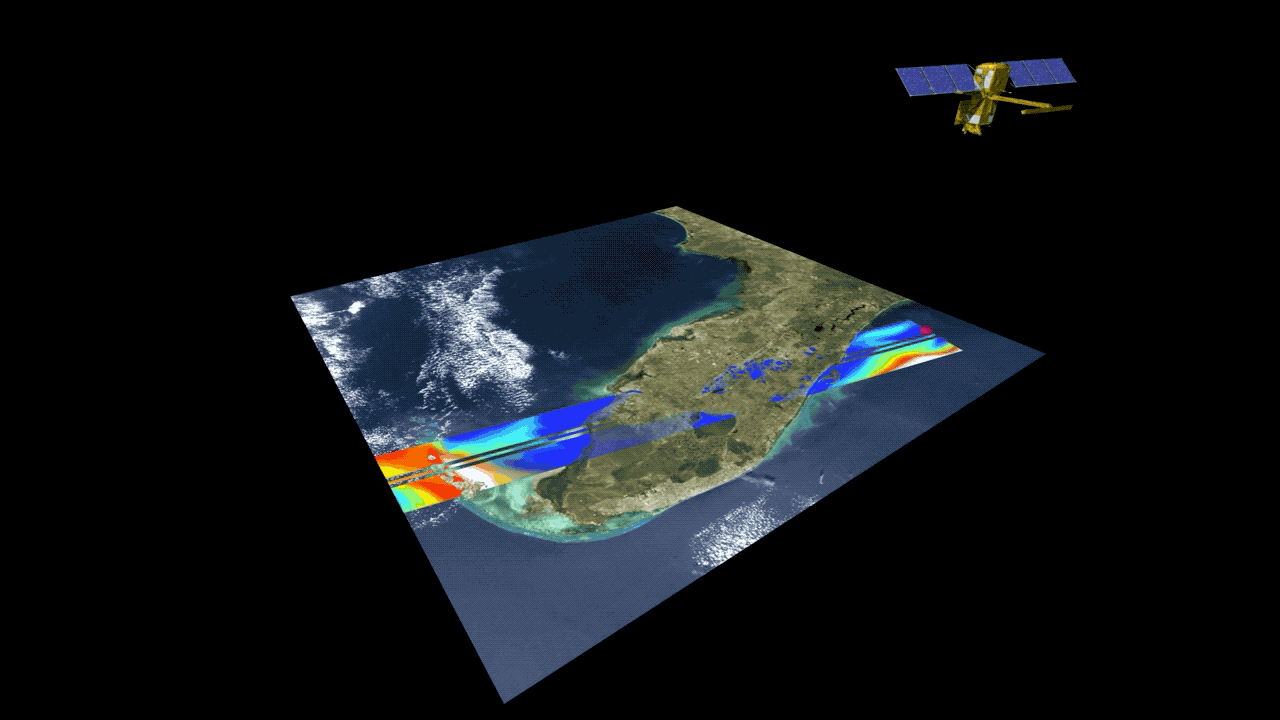
This animation shows the collection of data over the state of Florida, which is rich with rivers, lakes and wetlands. Credits: NASA/JPL-Caltech | + Expand image

Illustration of NASA’s Transiting Exoplanet Survey Satellite (TESS). Credits: NASA | + Expand image
How It Works
Dividing any circle’s circumference by its diameter gives you an answer of pi, which is usually rounded to 3.14. Because pi is an irrational number, its decimal representation goes on forever and never repeats. In 2021, a supercomputer calculated pi to more than 62 trillion digits. But you might be surprised to learn that for space exploration, NASA uses far fewer digits of pi.
Here at NASA, we use pi to understand how much signal we can receive from a distant spacecraft, to calculate the rotation speed of a Mars helicopter blade, and to collect asteroid samples. But pi isn’t just used for exploring the cosmos. Since pi can be used to find the area or circumference of round objects and the volume or surface area of shapes like cylinders, cones, and spheres, it is useful in all sorts of ways. Architects use pi when designing bridges or buildings with arches; electricians use pi when calculating the conductance of wire; and you might even want to use pi to figure out how much frozen goodness you are getting in your ice cream cone.
In the United States, March 14 can be written as 3.14, which is why that date was chosen for celebrating all things pi. In 2009, the U.S. House of Representatives passed a resolution officially designating March 14 as Pi Day and encouraging teachers and students to celebrate the day with activities that teach students about pi. And that's precisely what the NASA Pi Day Challenge is all about!
The Science Behind the 2022 NASA Pi Day Challenge
This ninth installment of the NASA Pi Day Challenge includes four brain-busters that get students using pi to measure frost deep within craters on the Moon, estimate the density of Mars’ core, calculate the water output from a dam to assess its potential environmental impact, and find how far a planet-hunting satellite needs to travel to send data back to Earth.
Read on to learn more about the science and engineering behind the problems or click the link below to jump right into the challenge.
› Take the NASA Pi Day Challenge
› Educators, get the lesson here!
Lunar Logic
NASA’s Lunar Flashlight mission is a small satellite that will seek out signs of frost in deep, permanently shadowed craters around the Moon’s south pole. By sending infrared laser pulses to the surface and measuring how much light is reflected back, scientists can determine which areas of the lunar surface contain frost and which are dry. Knowing the locations of water-ice on the Moon could be key for future crewed missions to the Moon, when water will be a precious resource. In Lunar Logic, students use pi to find out how much surface area Lunar Flashlight will measure with a single pulse from its laser.
Core Conundrum
Since 2018, the InSight lander has studied the interior of Mars by measuring vibrations from marsquakes and the “wobble” of the planet as it rotates on its axis. Through careful analysis of the data returned from InSight, scientists were able to measure the size of Mars’ liquid core for the first time and estimate its density. In Core Conundrum, students use pi to do some of the same calculations, determining the volume and density of the Red Planet’s core and comparing it to that of Earth’s core.
Dam Deduction
The Surface Water and Ocean Topography, or SWOT mission will conduct NASA's first global survey of Earth's surface water. SWOT’s state-of-the-art radar will measure the elevation of water in major lakes, rivers, wetlands, and reservoirs while revealing unprecedented detail on the ocean surface. This data will help scientists track how these bodies of water are changing over time and improve weather and climate models. In Dam Deduction, students learn how data from SWOT can be used to assess the environmental impact of dams. Students then use pi to do their own analysis, finding the powered output of a dam based on the water height of its reservoir and inferring potential impacts of this quick-flowing water.
Telescope Tango
The Transiting Exoplanet Survey Satellite, or TESS, is designed to survey the sky in search of planets orbiting bright, nearby stars. TESS does this while circling Earth in a unique, never-before-used orbit that brings the spacecraft close to Earth about once every two weeks to transmit its data. This special orbit keeps TESS stable while giving it an unobstructed view of space. In its first two years, TESS identified more than 2,600 possible exoplanets in our galaxy with thousands more discovered during its extended mission. In Telescope Tango, students will use pi to calculate the distance traveled by TESS each time it sends data back to Earth.
Teach It
Celebrate Pi Day by getting students thinking like NASA scientists and engineers to solve real-world problems in NASA Pi Day Challenge. Completing the problem set and reading about other ways NASA uses pi is a great way for students to see the importance of the M in STEM.
Pi Day Resources
-

Pi in the Sky Lessons
Here's everything you need to bring the NASA Pi Day Challenge into the classroom.
Grades 4-12
Time Varies
-

NASA Pi Day Challenge
The entire NASA Pi Day Challenge collection can be found in one, handy slideshow for students.
Grades 4-12
Time Varies
-

How Many Decimals of Pi Do We Really Need?
While you may have memorized more than 70,000 digits of pi, world record holders, a JPL engineer explains why you really only need a tiny fraction of that for most calculations.
-

18 Ways NASA Uses Pi
Whether it's sending spacecraft to other planets, driving rovers on Mars, finding out what planets are made of or how deep alien oceans are, pi takes us far at NASA. Find out how pi helps us explore space.
-
10 Ways to Celebrate Pi Day With NASA on March 14
Find out what makes pi so special, how it’s used to explore space, and how you can join the celebration with resources from NASA.
-

Infographic: Planet Pi
This poster shows some of the ways NASA scientists and engineers use the mathematical constant pi (3.14) and includes common pi formulas.
-

Downloads
Can't get enough pi? Download this year's NASA Pi Day Challenge graphics, including mobile phone and desktop backgrounds:
- Pi in the Sky 9 Poster (PDF, 11.2 MB)
- Lunar Flashlight Background: Phone | Desktop
- Mars InSight Lander Background: Phone | Desktop
- SWOT Mission Background: Phone | Desktop
- TESS Mission - Downlink Background: Phone | Desktop
- TESS Mission - Science Background (not pictured): Phone | Desktop
- Medley Background (not pictured): Phone | Desktop
-
Pi Day: What's Going 'Round
Tell us what you're up to this Pi Day and share your stories and photos on our showcase page.
Plus, join the conversation using the hashtag #NASAPiDayChallenge on Facebook, Twitter, and Instagram.
Recursos en español
Related Lessons for Educators
-

Planetary Egg Wobble and Newton's First Law
Students try to determine the interior makeup of an egg (hard-boiled or raw) based on their understanding of center of mass and Newton’s first law of motion.
Grades 3-8
Time 30 min to 1 hour
-

Whip Up a Moon-Like Crater
Whip up a moon-like crater with baking ingredients as a demonstration for students.
Grades 1-6
Time 30 min to 1 hour
-

Exploring Exoplanets with Kepler
Students use math concepts related to transits to discover real-world data about Mercury, Venus and planets outside our solar system.
Grades 6-12
Time 30 min to 1 hour
-

Tracking Water Using NASA Satellite Data
Using real data from NASA’s GRACE satellites, students will track water mass changes in the U.S.
Grades 4-8
Time 30 min to 1 hour
-
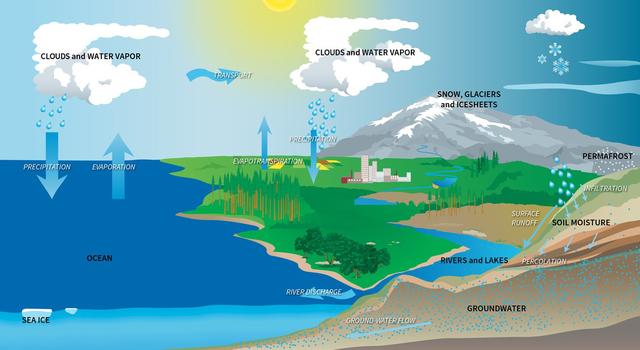
Modeling the Water Budget
Students use a spreadsheet model to understand droughts and the movement of water in the water cycle.
Grades 5-8
Time 30 min to 1 hour
Related Activities for Students
-
NASA's Earth Minute: Mission to Earth?
NASA doesn't just explore outer space! It studies Earth, too, with a fleet of spacecraft and scientists far and wide.
Type Video
Subject Science
-

Look at the Moon! Journaling Project
Draw what you see in a Moon Journal and see if you can predict the moon phase that comes next.
Type Project
Subject Science
-

Mars in a Minute: Are There Quakes on Mars?
Are there earthquakes on Mars – or rather, "marsquakes"? What could they teach us about the Red Planet?
Type Video
Subject Science
Explore More
Infographic
Facts and Figures
Missions and Instruments
Websites
TAGS: Pi Day, Pi, Math, NASA Pi Day Challenge, Moon, Lunar Flashlight, Mars, InSight, Earth, Climate, SWOT, Exoplanets, Universe, TESS, Teachers, Educators, Parents, Students, Lessons, Activities, Resources, K-12
Edu News | December 6, 2021
The Best New STEM Education Resources from NASA-JPL in 2021
In 2021, we added nearly 80 STEM education resources to our online catalog of lessons, activities, articles, and videos for educators, students, and families. The resources feature NASA's latest missions exploring Earth, the Moon, Mars, asteroids, the Solar System and the universe beyond. Here are the 10 resources our audiences visited most this year.
NASA's Mission to Mars Student Challenge
To kick off the year, we invited students, educators, and families from around the world to create their own mission to Mars as we counted down to the Perseverance rover's epic landing on the Red Planet in February. More than one million students participated in the Mission to Mars Student Challenge, which features seven weeks of guided education plans, student projects, and expert talks and interviews highlighting each phase of a real Mars mission.
It's no surprise that this was our most popular product of the year. And good news: It's still available and timely! With Perseverance actively exploring Mars and making new discoveries all the time, the challenge offers ongoing opportunities to get students engaged in real-world STEM.
Need a primer on the Perseverance Mars rover mission, first? This article from our Teachable Moments series has you covered.
Solar System Size and Distance
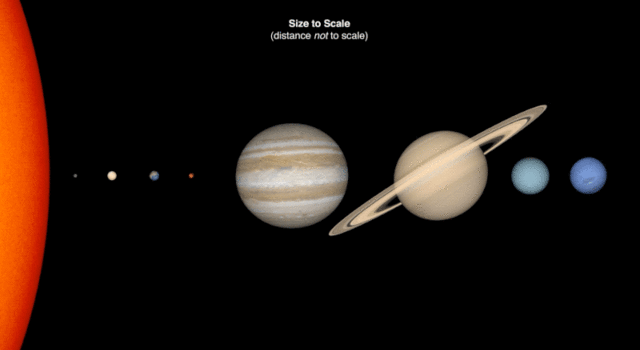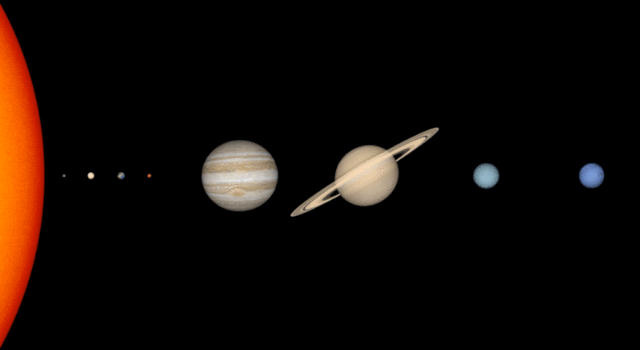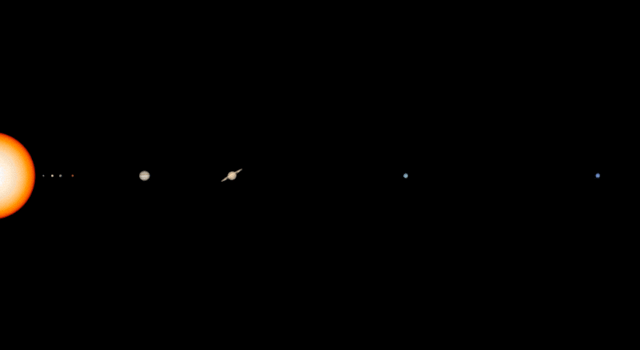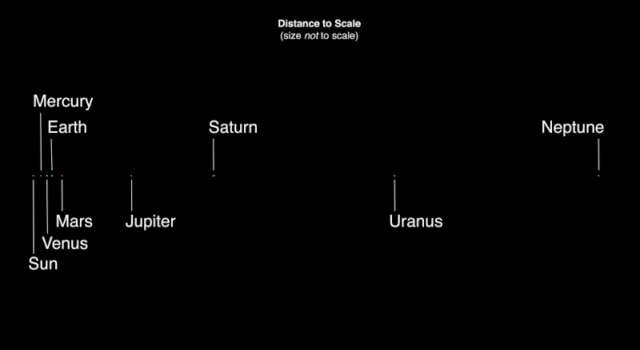
This video offers a short and simple answer to two of students' most enduring questions: How do the sizes of planets compare and how far is it between them? Plus, it gets at why we don't often (or ever) see images that show all the planets' sizes and distances to scale. Spoiler alert: It's pretty much impossible to do.
Get students exploring solar system size and distance in more detail and even making their own scale models with this student project.
Code a Mars Helicopter Video Game
As you'll soon see from the rest of this list, coding projects were a big draw this year. This one took off along with Ingenuity, the first helicopter designed to fly on Mars, which made its historic first flight in April. Designed as a test of technology that could be used on future missions, Ingenuity was only slated for a few flights, but it has far exceeded even that lofty goal.
In this project, students use the free visual programming language Scratch to create a game inspired by the helicopter-that-could.
Make a Moon Phases Calendar and Calculator
Just updated for 2022, this project is part educational activity and part art for your walls. Students learn about moon phases to complete this interactive calendar, which shows when and where to see moon phases throughout the year, plus lists moon events such as lunar eclipses and supermoons. The art-deco inspired design might just have you wanting to make one for yourself, too.
The NASA Pi Day Challenge
This year marked the eighth installment of our annual Pi Day Challenge, a set of illustrated math problems featuring pi (of course) and NASA missions and science. Don't let the name fool you – these problems are fun to solve year round.
Students can choose from 32 different problems that will develop their math skills while they take on some of the same challenges faced by NASA scientists and engineers. New this year are puzzlers featuring the OSIRIS-REx asteroid mission, Mars helicopter, Deep Space Network, and aurora science.
Educator guides for each problem and problem set are also available here. And don't miss the downloadable posters and virtual meeting backgrounds.
Code a Mars Sample Collection Video Game
Another coding challenge using the visual programming language Scratch, this project is inspired by the Perseverance Mars rover mission, which is collecting samples that could be brought back to Earth by a potential future mission.
While developing a gamified version of the process, students are introduced to some of the considerations scientists and engineers have to make when collecting samples on Mars.
Code a Mars Landing
As if launching a rover to Mars wasn't hard enough, you still have to land when you get there. And that means using a complex series of devices – from parachutes to jet packs to bungee cords – and maneuvers that have to be performed remotely using instructions programmed into the spacecraft's computer.
Students who are ready to take their programming skills to the next level can get an idea of what it takes in this project, which has them use Python and microcontrollers to simulate the process of landing a rover on Mars.
How Far Away is Space?
Without giving the answer away: It's not as far as you might think.
In this activity, students stack coins (or other objects) on a map of their local area as a scale model of the distance to space. The stacking continues to the International Space Station, the Moon, and finally to the future orbit of the James Webb Space Telescope, which is slated to launch on Dec. 22.
Build a Rover and More With Shapes
You don't have to be a big kid to start learning about space exploration. This activity, which is designed for kids in kindergarten through second grade, has learners use geometric shapes called tangrams to fill in a Mars rover design. It provides an introduction to geometry and thinking spatially.
Once kids become experts at building rovers, have them try building rockets.
Space Voyagers: The Game
Technically a classroom activity (it is standards-aligned, after all), this game will appeal to students and strategy card game enthusiasts alike. Download and print out a set for your classroom (or your next game night).
Players work collaboratively to explore destinations including the Moon, Mars, Jupiter and Jupiter's Moon Europa with actual NASA spacecraft and science instruments while working to overcome realistic challenges at their destination including dust storms and instrument failures.
TAGS: K-12, Lessons, Activities, Education Resources, Teachers, Students, Families, Kids, Learning, STEM, Science, Engineering, Technology, Math, Coding, Programming, Mars, Solar System, Moon
Career Guidance | August 19, 2021
How to Get an Internship at JPL
Whether you're looking for a career in STEM or space exploration, this three-part series will cover everything you need to know about the world of internships at NASA's Jet Propulsion Laboratory, the skills and experience hiring managers are looking for, and how you can set yourself on the right trajectory even before you get to college.
In a typical year, NASA's Jet Propulsion Laboratory brings in about 1,000 interns from schools across the country to take part in projects that range from building spacecraft to studying climate change to developing software for space exploration. One of 10 NASA centers in the United States, the Southern California laboratory receives thousands of applications. So what can students do to stand out and set themselves on the right trajectory?
We asked interns and the people who bring them to JPL about their tips for students and anyone interested in a STEM career or working at the Laboratory. We're sharing their advice in this three-part series.
First up: Learn about the kinds of opportunities available as well as where and how to apply.
The World of JPL Internships
If you found this article, you're probably already somewhat familiar with the work that goes on at JPL. But at a place that employs more than 6,000 people across hundreds of teams, it can be hard to keep track of it all.
In a broad sense, JPL explores Earth, other planets, and the universe beyond with robotic spacecraft – meaning no humans on board. But along with the engineers and scientists who design and build spacecraft and study the data they return, there are thousands of others working on all the in-between pieces that make Earth and space exploration possible and accessible to all. This includes software developers, machinists, microbiologists, writers, video producers, designers, finance and information technology professionals, and more.
Some of the best ways to learn about the Laboratory's work – and get a sense for the kinds of internships on offer – are to follow JPL news and social media channels, take part in virtual and in-person events such as monthly talks, and keep up on the latest research. There are also a host of articles and videos online about interns and employees and the kinds of work they do.
While STEM internships make up the majority of the Laboratory's offerings, there are a handful of opportunities for students studying other subjects as well. Depending on which camp you fit into, there are different places to apply.
Education Office Internships
The largest number of internships can be found on the JPL Education website. These opportunities, for students studying STEM, are offered through about a dozen programs catered to college students of various academic and demographic backgrounds. This includes programs for students attending community college, those at minority-serving institutions, and others at Los Angeles-area schools.
Students apply to a program, or programs, rather than a specific opening. (See the program details for more information about where to apply and what you will need.) It's then up to the folks with open opportunities, the mentors, to select applicants who are the best match for their project.
It may seem odd to send an application into the void with no idea of what offer might return. But there is a good reason behind the process, says Jenny Tieu, a project manager in JPL's Education Office, which manages the Laboratory's STEM internship programs.
"Applying to a specific program allows for the applicant to be seen by a much broader group of hiring managers and mentors and be considered for more opportunities as a result," says Tieu. "We look at the resumes that come in to see what skills are compatible with open projects and then match students to opportunities they may not have even realized were available to them."
Shirin Nataneli says she wouldn't have known there was an internship for her at the Laboratory were it not for a suggestion to apply from her professor. In 2020, Nataneli graduated from UCLA with a Bachelor's degree in biology. She was on the pre-med track, studying for the MCAT, when she decided to take a couple of courses in computer science.
"I got sucked in," says the Santa Monica College student and JPL intern, who is using computer science to help her team classify extreme bacteria that can survive on spacecraft. "I didn't even know there was an intersection between computer science and biology, but somehow I found a group at JPL that does just that."

Shirin Nataneli poses for a photo with the JPL campus in the background. Image courtesy: Shirin Nataneli | + Expand image
University Recruiting Opportunities
For college students who are interested in space exploration but studying other fields, such as business, communications, and finance, as well as those studying STEM, there are additional opportunities on the JPL Jobs website. Listed by opportunity, more like a traditional job opening, these internships are managed by the Laboratory's University Recruiting team, which is active on LinkedIn and Instagram and can often be found at conferences and career fairs.
The When, What, and Where
Both Education Office and University Recruiting opportunities are paid and require a minimum 3.00 GPA, U.S. citizenship or legal permanent resident status, as well as an initial commitment of 10 weeks. Applicants must be enrolled in a college undergraduate or graduate program to be eligible. (See "The Pre-College Trajectory" section of this article below to learn about what high-school and younger students can do to prepare for a future JPL internship or STEM career.)
After pivoting to fully remote internships during the COVID-19 pandemic, JPL has continued to offer some remote or hybrid internships now that the Los Angeles-area campus has opened back up.
"We know that remote internships are effective," says Tieu. "Interns have said that they're able to foster connections with JPL employees and gain valuable experience even from home." She notes that while in-person internships give students maximum exposure to JPL – including visits to Laboratory attractions like mission control, the "clean room" where spacecraft are built, and a rover testing ground called the Mars Yard – remote internships have had a positive impact on students who previously weren't able to participate in person due to life constraints.
Most programs offer housing and travel allowances to students attending universities outside the 50-mile radius of JPL, so be sure to check the program details if traveling to or living in the Los Angeles area could be tricky financially.
Full-time and part-time opportunities can be found throughout the year with most openings in the summertime for full-time interns, meaning 40 hours per week. For summer opportunities, Tieu recommends applying no later than November or December. Applicants can usually expect to hear back by April if they are going to receive an offer for summer, but it's always a good idea to keep yourself in the running, as applicants may be considered for school-year opportunities.
Tieu adds, "If you haven't heard back, and you're closing in on the six-month mark of when you submitted your application, I recommend students go back in and renew their application [for the programs listed on the JPL Education website] so that it remains active in the candidate pool for consideration."
And unlike job applications, where it's sometimes frowned upon to apply to multiple positions at once, it's perfectly alright – and even encouraged – to apply to multiple internships.
You may also want to consider these opportunities, especially if you're looking for internships at other NASA centers, you're a foreign citizen, or you're interested in a postdoc position:
- NASA Internships
- JPL Visiting Student Researcher Program (international students eligible)
- JPL Postdoctoral Study
The most important thing is to not count yourself out, says Tieu. "If you're interested, work on that resume, get people to review your resume and provide input and feedback and apply. We don't expect students to come in knowing how to do everything. We're looking for students with demonstrated problem-solving, teamwork, and leadership skills. Software and other technical skills are an added bonus and icing on the cake."
More on that next, plus advice from JPL mentors on the skills and experience they look for from potential interns.
Skills for Space Explorers
JPL is known for doing the impossible, whether it's sending spacecraft to the farthest reaches of our solar system or landing a 2,000-pound rover on Mars. But potential applicants may be surprised to learn that reputation wasn't earned by always having the right answer on the first try – or even the second, third, or fourth.

JPL's founders, several Caltech graduate students led by Frank Malina along with rocket enthusiasts from the Pasadena area, take a break from setting up their experimental rocket motor in the Arroyo Seco, north of Pasadena, California. Image credit: NASA/JPL-Caltech | + Expand image
In fact, the Laboratory has always had a penchant for experimentation, starting with its founders, Caltech students who in the 1930s would test rockets in the stairwells at their university. They had so many colossal (and dangerous) failures that they were banished to a dry riverbed north of Pasadena, which is now the site of JPL. Eventually, their rockets were successful and the laboratory they founded went on to build and launch the first American space satellite and send dozens of spacecraft to worlds throughout the solar system. But that trial-and-error attitude still permeates the Laboratory today.
As a result, potential interns who show enthusiasm and a willingness to learn, overcome obstacles, and work as part of a team often stand out more than those with academic achievements alone.
Standing Out
In an informal survey of JPL mentors, respondents most often cited problem-solving, communication, and teamwork skills as well as passion for learning and grit as the soft skills they look for when considering potential interns. Respondents added that students who can provide specific examples of these skills on their resume – and speak to them in an interview – stand out the most.
That doesn't necessarily have to mean leading your school’s robotics club or serving as your geology professor's teaching assistant, although those things don't hurt. But also consider less traditional examples, such as how critical thinking helps you overcome challenges while rock climbing or how you used leadership and teamwork to organize your friends to create a group costume for Comic Con.
"Students who share a link to their GitHub repository or online portfolio stand out to me because it shows they took the initiative and took time to build, develop, and create something on their own," says K'mar Grant-Smith, a JPL mentor who leads a team of developers in supporting and maintaining applications for the Laboratory's missions. "That vouches for you better than saying, 'I know these [coding] languages, and I took these courses.'"
Laurie Barge is a JPL scientist who co-leads an astrobiology lab exploring the possibility of life beyond Earth. The lab annually hosts about a dozen students and postdocs. Barge says that the top qualities she looks for in an intern are an expressed interest in her research and JPL as a whole as well as teamwork skills. "I look for students who are excited about the fact that they'll be working with 10 other students and postdocs and collaborating with other people on papers and abstracts."

Astrobiologist Laurie Barge, left, and former intern Erika Flores, right, pose for a photo in the Origins and Habitability Lab that Barge co-leads at JPL. Image credit: NASA/JPL-Caltech | + Expand image
Teamwork is also key for students working in engineering, software, or any other capacity across the Laboratory. When it comes to designing missions to go where nothing has gone before, collaboration between multi-disciplinary teams is a must.
In terms of technical skills, knowledge of coding languages is the most sought after, with Python, MATLAB, and C languages leading the pack. And in certain groups, like the one that helps identify where it's safe to land spacecraft on Mars, experience with specialized tools like Geographic Information Systems, or GIS, can help applicants stand out.
Still, for many mentors, enthusiasm and a willingness to learn and be proactive are far more important than any technical skill.
"You don't have to be the most technically savvy person. If you have the initiative, the drive, and some experience, I find that to be more important than knowing 16 different [coding] languages," says Grant-Smith. "JPL is a unique place full of very smart people, but we're not good at what we do just because we have the know-how. We also have the drive and a passion for it."
Getting Involved
So you're a rock-climbing Red Planet enthusiast who likes to create "Dune"-inspired stillsuits when you're not busy at your part-time job making frappuccinos with your fellow baristas. How do you improve the chances this information will land on a JPL mentor's desk?
In a sentence: Build a strong network. So says Rebecca Gio of what made all the difference when she was struggling to find her academic groove right after high school. After a year spent repeating classes, changing schools, and feeling discouraged about what was next, Gio discovered what she needed to change her trajectory. She joined clubs and organizations that aligned with her career goals, formed study groups with her peers, found a mentor who could help her navigate everything from college classes to internship opportunities, and wasn't afraid to ask when she had a question.
Now, Gio is thriving – academically and on her career path. She's a junior studying computer science at Cal Poly Pomona and a first-time intern at JPL, where she's testing the software that will serve as the brains of a spacecraft designed to explore Jupiter's moon Europa.
"Being part of a community and being with people who have gone through similar experiences and can push you to do better, I think that that is just super motivating," says Gio.
JPL Education Program Manager Jenny Tieu agrees. “Along with academic achievements, we’re looking for students with diverse backgrounds, perspectives, and life experiences who can work collaboratively to learn, adapt to new situations, and solve problems.”

Jenny Tieu catches up with Brandon Murphy, who came to the Laboratory as an intern in 2016 through a program Tieu manages, and soon after, was hired full-time. Image credit: NASA/JPL-Caltech | + Expand image
To that end, she suggests students get involved in campus STEM clubs and communities, NASA challenges and activities, and volunteer opportunities, which offer career experiences, introduce students to a network of peers and professionals, and look great on a resume.
Tieu leads a JPL internship program that partners with historically Black colleges and universities and other minority-serving institutions. She says that one way students get connected with the program is by word-of-mouth from current and former participants, who include students and faculty researchers.
"We see a lot of great allyship with interns and research fellows telling their classmates about their experience at JPL, how to apply, and what to expect," says Tieu. "We foster deep relationships with our partner campuses and their faculty as well." In other words, students may not have to look farther than their own professors, campus info sessions, or career fairs to learn about opportunities at the Laboratory.
A career fair is where Gio first connected with JPL's University Recruiting team after what she jokingly calls "stalking" them from LinkedIn to Handshake to the Grace Hopper conference – where she eventually handed over her resume. "Just get familiar with where JPL is going to be and try to make sure that you're there," says Gio.

Rebecca Gio (right) poses for a photo with her mom and sister (left) in the lobby of the Laboratory's mission control building during the Explore JPL event in 2019. Gio says her mom and sister are her two biggest supporters and the reason behind all of her success. Image courtesy Rebecca Gio | + Expand image
In the sciences especially, those connections can also be made through a shared interest in a particular area of research. Barge says that most of the students she brings to JPL find out about her research from a peer or professor, exploring the lab's website, or from reading papers her team has published. Then, they reach out to her directly. This way she can create a position suited to a student's skills while also finding out if their interests mesh with the team.
"I want to know why they're interested in JPL and not a different institution," says Barge. "Why do they want to work with me and not another person at JPL? Why do they want to do this research and what specifically would they like to gain from this internship experience? I'm trying to figure out who really, really wants this particular opportunity."
As Gio points out, it's often the same advice that applies whether you're looking for an internship at JPL or in STEM or a future career.
"If you really want it, if you really want to be a STEM professional, make the most of your education, and find ways to apply those skills," says Gio. "I made sure that I was a part of campus groups where I was doing extra projects outside of schoolwork. I made sure that I was talking to other students to learn what they were doing. There's a lot of opportunities now to learn online for free. If there's something that you think would interest you, just go and do it."
Next, we'll share more ways students can prepare for a future internship or career in STEM before they get to college, plus resources parents and teachers can use to get younger students practicing STEM skills.
The Pre-College Trajectory
First, let's address one of the most common questions we get when it comes to internships at JPL. As of this writing, the Laboratory does not offer an open call for high-school interns. For most of the past several years, JPL has been able to bring in just a handful of high-school students from underserved communities thanks to partnerships with local school districts.
That's not to say that there won't be an open call for high-school internships at JPL in the future. If and when opportunities become available, they'll be posted here on the JPL Education website.
That said, there's still plenty students can and should do before college or when they're just entering college to explore STEM fields, get hands-on experience, and practice the skills they'll need for a future internship or career.
Exploring STEM Fields
Ota Lutz, a former classroom teacher, leads JPL's K-12 education team, which takes the Laboratory's science, engineering, and technical work and translates it into STEM education resources for teachers, students, and families.
Other than exploring high-school internships at other organizations, Lutz says that students in grades K-12 can get hands-on experience through clubs, competitions, and camps offered in person and online.
Schools often have engineering, robotics, math, and science clubs, but if not, look for one in your community or encourage students to start their own, perhaps with the help of a teacher.

JPL's Invention Challenge is an annual engineering competition for middle and high school students. In 2017, a team (pictured) traveled all the way from Ethiopia to participate. | › Read the news story
JPL hosts annual science and engineering competitions while NASA hosts a slew of other competitions, including essay contests with opportunities to interact with scientists and even name spacecraft.
If cost is an issue for camps or competitions, Lutz recommends that parents or guardians reach out to the host organization to see if scholarships are available and that they explore free events offered by groups such as NASA's Solar System Ambassadors and Night Sky Network as well as programs at museums, science centers, and libraries in their community.
NASA also offers a number of citizen science projects that give students (and adults) opportunities to contribute to real research, from identifying near-Earth asteroids to observing and cataloging clouds to searching for planets beyond our solar system.
Building Foundational Skills
All of the above can help students explore whether they might be interested in STEM, but it's also important that kids start practicing the skills they will need to succeed academically and in a future internship or career.
"Developing those foundational STEM and language arts skills is incredibly important to future success," says Lutz, adding that, generally, students should practice what are called scientific habits of mind, "learning how to think critically, problem solve and do so in a methodical way as well as learning to examine data to determine trends without personal bias."
One way students can gain skills and knowledge directly related to a future STEM internship or career is by trying these educational projects and activities offered free online from the JPL Education Office. (Teachers can explore this page to find out how to turn these activities into standards-aligned classroom lessons.) Activities include engineering projects and science experiments as well as math and coding challenges, all of which feature the latest NASA missions and science.

Students test their designs as part of the "Make an Astronaut Lander" activity on the JPL Education website. | + Expand image
Coding skills, in particular, will serve students well no matter what career path they take, says Lutz. "Coding is something that is applicable across a broad range of subject areas and majors, so we strongly encourage students to learn some coding."
She points to the plethora of online courses and tutorials in coding and other STEM subjects that give students a chance to explore on their own and work on projects that interest them.
Parents and guardians can also help their kids develop foundational skills by allowing them to explore and tinker at home. "In every house, there's something that needs fixing," says Lutz. "Have the kid figure out how to fix a wobbly chair, but be patient with mistakes and encourage them to keep trying." That persistence and determination in overcoming obstacles will come in handy throughout their education and career path, whether it's learning how to code, getting into a robotics club in high school, applying and reapplying for internships, or figuring out how to land a spacecraft on Mars.
Similarly, it's never too early to start learning those ever-important soft skills such as teamwork, communication, and leadership. There's no single or right place to gain these skills, rather they come from a range of experiences that can include a school project, a part-time job, or a volunteer opportunity.

Ota Lutz, who leads the Laboratory's K-12 education team, speaks with a group of JPL employees during a Pi Day event. | + Expand image
Lutz grew up in a small town in Central California and says, "I was a smart kid, but these things called soft skills were beyond me, and I was the shyest kid in my class." That is until she joined her high school's service club. "Through volunteering, I ended up interacting with people from all walks of life and learned how to work with teams. My club advisor coached me, and I started taking on more leadership roles in the club and in class projects."
Later, it was that same club advisor and her youth pastor who encouraged Lutz to attend a college that would challenge her academically despite pressures to stay closer to home.
"You never know what experiences or conversations might open up opportunities for you," says Lutz, which is why she recommends that students get comfortable talking with peers and teachers – and especially asking questions. "It's really important to learn to ask questions so you build your confidence in learning and also develop relationships with people."
Launching into College
As Lutz experienced, those foundational skills can make all the difference when it comes to transitioning into college, too.
"When I got to college, I discovered I was woefully unprepared even though I had been at the top of my class in high school," says Lutz. "I never learned how to study, and I mistakenly believed that asking questions would make me look dumb. After struggling on my own for a couple of years, I learned that study groups existed and they helped me get to know my peers, build my confidence, and improve my GPA."
While building a support network is key, don't overload yourself the first year, Lutz says. But do start taking classes in the field you're interested in to see if it's the right fit. "The important thing is getting some experience in the field that you think you want to go into."
After that, internships, whether they're at JPL, NASA or elsewhere, will give you an even deeper look at what a future career might be like. When the time comes, you'll know exactly where to look to set yourself on the right trajectory – that is just above under "The World of JPL Internships" and "Skills for Space Explorers."
The laboratory’s STEM internship and fellowship programs are managed by the JPL Education Office. Extending the NASA Office of STEM Engagement’s reach, JPL Education seeks to create the next generation of scientists, engineers, technologists and space explorers by supporting educators and bringing the excitement of NASA missions and science to learners of all ages.
Career opportunities in STEM and beyond can be found online at jpl.jobs. Learn more about careers and life at JPL on LinkedIn and by following @nasajplcareers on Instagram.
TAGS: Internships, Students, Careers, Science, Computer Science, Engineering, Math, Programs, University Recruiting, Undergraduate, Graduate, College, High School, Mentors

































