Lyle Tavernier is an educational technology specialist at NASA's Jet Propulsion Laboratory. When he’s not busy working in the areas of distance learning and instructional technology, you might find him running with his dog, cooking or planning his next trip.
Teachable Moments | March 18, 2024
The Science of Solar Eclipses and How to Watch With NASA
Get ready for the April 8 total solar eclipse. Learn about the science behind solar eclipses, how to watch safely, and how to engage students in NASA science.
On April 8, 2024, a total solar eclipse will be visible across much of the central and northeastern United States, as well as parts of Mexico and Canada.
Whether you are traveling to the path of the total eclipse or will be able to step outside and watch the eclipse where you live, here's everything you need to know, including what to expect, how to watch safely, and how to engage in scientific observations and discovery with NASA.
What Are Solar Eclipses?
Solar eclipses occur when the Sun, the Moon, and Earth align. For this alignment to happen, two things need to be true. First, the Moon needs to be in the new moon phase, which is when the Moon’s orbit brings it between Earth and the Sun. Second, eclipses can only happen during eclipse seasons, which last about 34 days and occur just shy of every six months. An eclipse season is the time period when the Sun, the Moon, and Earth can line up on the same plane as Earth's orbit during a new or full moon. If a new moon happens during an eclipse season, the shadow cast by the Moon will land on Earth, resulting in a solar eclipse. Most of the time, because the Moon’s orbit is slightly tilted, the Moon’s shadow falls above or below Earth, and we don't get a solar eclipse.
Not all solar eclipses look the same. The distance between the Sun, the Moon, and Earth plays an important role in what we see during a solar eclipse. Even though the Moon is much smaller than the Sun (about 400 times smaller in diameter), the Sun and Moon look about the same size from Earth. This is because the Sun is about 400 times farther away than the Moon. But as the Moon travels its elliptical orbit around Earth, its size appears slightly larger when it is closer to Earth and slightly smaller when it is farther from Earth. This contributes to the different kinds of solar eclipses you might have heard about. For example:
- During a total solar eclipse, the Moon is closer to Earth in its orbit and appears larger, completely blocking the Sun's disk. This allows viewers in the path of totality to see the Sun’s corona, which is usually obscured by the bright light of the Sun’s surface.
- An annular solar eclipse occurs when the Sun, Moon, and Earth are properly aligned, but the Moon is farther away in its orbit, so it does not completely cover the Sun's disk from our perspective. Annular eclipses are notable for the "ring of fire," a thin ring of the Sun’s disk that's still visible around the Moon during annularity. The name annular eclipse comes from the world of mathematics, where a ring shape is known as an annulus.
- Partial eclipses can happen for two reasons. First, viewers outside the path of totality during a total solar eclipse – or the path of annularity during an annular eclipse – will see only part of the Sun’s surface covered by the Moon. The other time a partial eclipse can occur is when the Moon is nearly above or below Earth in its orbit so only part of the Moon’s shadow falls on Earth. In this case, only part of the Sun’s surface will appear covered by the Moon.

This image of a total solar eclipse was captured on Aug. 21, 2017 from Madras, Oregon. Image credit: NASA/Aubrey Gemignani | › Full image and caption

On Jan. 4, 2017, the Hinode satellite captured these breathtaking images of an annular solar eclipse. Image credit: Hinode/XRT | › Full image and caption

The Sun appears partially eclipsed in this series of photos taken from NASA’s Johnson Space Center in Houston on Aug. 21, 2017. Image credit: NASA/Noah Moran | › Full image and caption
How to Watch the Upcoming Solar Eclipse
First, an important safety note: Do not look directly at the Sun or view any part of the partial solar eclipse without certified eclipse glasses or a solar filter. Read more below about when you can safely view the total solar eclipse without eclipse glasses or a solar filter. Visit the NASA Eclipse website for more information on safe eclipse viewing.
When following proper safety guidelines, witnessing an eclipse is an unparalleled experience. Many “eclipse chasers” have been known to travel the world to see solar eclipses. Here's what to expect on April 8, 2024:
The start time and visibility of the eclipse will depend on your location. You can use the interactive map below to find detailed eclipse information, including timing and coverage, by entering in your location. A list of some of the cities and start times along the path of totality is available on the NASA Science website.
Explore when and where to view the eclipse with this interactive map from NASA. Enter your zip code to see what will be visible in your viewing location and when to watch. Credit: NASA's Scientific Visualization Studio
The eclipse begins when the edge of the Moon first crosses in front of the disk of the Sun. This is called a partial eclipse and might look as if a bite has been taken out of the Sun.
It is important to keep your eclipse glasses on during all parts of the partial solar eclipse. The visible part of the Sun is tens of thousands of times brighter than what you see during totality. You can also use a pinhole camera to view the eclipse.
An approximately 115-mile-wide strip known as the path of totality is where the shadow of the Moon, or umbra, will fall on Earth. Inside this path, totality will be visible starting about 65 to 75 minutes after the eclipse begins.
If you are in the path of totality, it is safe to take off your eclipse glasses and look at the total eclipse only during totality. Be sure to put your glasses back on before the total phase ends and the surface of the Sun becomes visible again. Your viewing location during the eclipse will determine how long you can see the eclipse in totality. In the U.S., viewers can expect to see 3.5 to 5.5 minutes of totality.
After totality ends, a partial eclipse will continue for 60 to 80 minutes, ending when the edge of the Moon moves off of the disk of the Sun.
For more information about the start of the partial eclipse, the start and duration of totality, and the percentage of the Sun eclipsed outside the path of totality, find your location on this eclipse map.
On April 8, NASA Television will host a live broadcast featuring expert commentary and views from telescopes along the path of totality. Tune into the broadcast from 10 a.m. to 1 p.m. PDT (1 to 4 p.m. EDT) on the day of the eclipse.
Join NASA as a total solar eclipse moves across North America on April 8. Tune in from 10 a.m. to 1 p.m. PDT (1 to 4 p.m. EDT) for live views from across the path, expert commentary, live demos, and more. | Watch on YouTube
What Solar Eclipses Mean for Science
Solar eclipses provide a unique opportunity for scientists to study the Sun and Earth from land, air, and space, plus allow the public to engage in citizen science!

NASA’s Solar and Heliospheric Observatory, or SOHO, constantly observes the outer regions of the Sun’s corona using a coronagraph. Image credit: ESA/NASA/SOHO | + Expand image
Scientists measure incoming solar radiation, also known as insolation, to better understand Earth’s radiation budget – the energy emitted, reflected, and absorbed by our planet. Just as clouds block sunlight and reduce insolation, eclipses create a similar phenomenon, providing a great opportunity to study how increased cloud cover can impact weather and climate.
Solar eclipses can also help scientists study solar radiation in general and the structure of the Sun. On a typical day, the bright surface of the Sun, called the photosphere, is the only part of the Sun we can see. During a total solar eclipse, the photosphere is completely blocked by the Moon, leaving the outer atmosphere of the Sun (corona) and the thin lower atmosphere (chromosphere) visible. Studying these regions of the Sun’s atmosphere can help scientists understand solar radiation, why the corona is hotter than the photosphere, and the process by which the Sun sends a steady stream of material and radiation into space. Annular solar eclipses provide opportunities for scientists to practice their observation methods so that they'll be ready when a total solar eclipse comes around.
Citizen scientists can get involved in collecting data and participating in the scientific process during the eclipse through NASA’s GLOBE program. Anyone in the path of the eclipse and in partial eclipse areas can act as citizen scientists by measuring temperature and cloud cover data and report it using the GLOBE Observer app to help further the study of how eclipses affect Earth’s atmosphere.
Visit NASA's Eclipse Science page to learn more about the many ways scientists are using the eclipse to improve their understanding of Earth, the Moon, and the Sun.
Taking Eclipse Science Farther
Eclipses also make a great jumping-off point to concepts and techniques used in astrophysics and our search for planets beyond our solar system.
Similar to a solar eclipse, a transit occurs when a planet crosses in front of the face of a star. From Earth, the planets Venus and Mercury can occasionally be seen transiting in front of the Sun, appearing as small, dark dots. Transits are also useful for detecting exoplanets – distant planets around other stars. When an exoplanet passes in between its star and Earth, we can measure tiny dips in the star's brightness that tell scientists a planet is there even when it’s too small to see.
Another way that eclipse concepts are used for astrophysics is with coronagraphs, mechanisms inside telescopes that block the light from a star. By creating a sort of artificial eclipse, coronagraphs help scientists search for exoplanets by making much dimmer planets orbiting a star easier to see. For example, NASA’s Nancy Grace Roman Telescope, slated for launch later this decade, will use an advanced coronagraph to analyze and directly image planets that orbit other stars. Learn more about the astrophysics involved in eclipses, including the use of gravitational lensing to study background objects, from NASA’s Universe of Learning.
Learn how the coronagraph instrument on the Nancy Grace Roman Telescope will allow the spacecraft to peer at the universe through some of the most sophisticated sunglasses ever designed. | Watch on YouTube
Solar Eclipse Lessons and Projects
Use these standards-aligned lessons, plus related activities and resources, to get your students excited about the eclipse and the science that will be conducted during the eclipse.
-
 Student Project
Student ProjectHow to Make a Pinhole Camera
Learn how to make your very own pinhole camera to safely see a solar eclipse in action from anywhere the eclipse is visible, partial or full!
Subject Science
Grades K-12
Time < 30 mins
-
 Collection
CollectionNASA's Universe of Learning – Eclipse Resources
Explore a curated collection of resources to expand student learning around the eclipse to related astrophysics concepts.
-
 Lesson
LessonMoon Phases
Students learn about the phases of the Moon by acting them out. In 30 minutes, they will act out one complete, 30-day, Moon cycle.
Subject Science
Grades 1-6
Time 30-60 mins
-
 Lesson
LessonModel a Solar Eclipse
Students use simple materials to model a partial, annular, and total solar eclipse.
Subject Science
Grades 1-8
Time 30-60 mins
-
 Lesson
LessonMeasuring Solar Energy During an Eclipse
Students use mobile devices to measure the impact a solar eclipse has on the energy received at Earth’s surface.
Subject Math
Grades 4-7
Time 1-2 hrs
-
 Lesson
LessonModeling the Earth-Moon System
Students learn about scale models and distance by creating a classroom-size Earth-Moon system.
Subject Science
Grades 6-8
Time 30-60 mins
-
 Math Problem
Math ProblemEpic Eclipse
Students use the mathematical constant pi to approximate the area of land covered by the Moon’s shadow during the eclipse.
Subject Math
Grades 6-12
Time < 30 mins
-
 Math Problem
Math ProblemEclipsing Enigma
Students use pi to figure out how much of the Sun’s disk will be covered by the Moon during an eclipse and whether it’s a total or annular eclipse.
Subject Math
Grades 7-12
Time < 30 mins
-
 Mobile App
Mobile AppNASA GLOBE Observer App
Students can become citizen scientists and collect data for NASA’s GLOBE Program using this app available for iOS and Android devices.
Explore More
Eclipse Info
- NASA Eclipses Website
- Calendar of Past and Upcoming Eclipses
- Downloadable Eclipse Map
- NASA HEAT Eclipse Training Slide Decks
Eclipse Safety
Interactives
Citizen Science
Facts & Figures
NASA's Universe of Learning materials are based upon work supported by NASA under award number NNX16AC65A to the Space Telescope Science Institute, working in partnership with Caltech/IPAC, Center for Astrophysics | Harvard & Smithsonian, and the Jet Propulsion Laboratory.
TAGS: Solar Eclipse, Eclipse, Annular Eclipse, K-12 Education, Lessons, Classroom Resources, STEM Resources
Teachable Moments | March 7, 2024
A Prime Year for NASA's Pi Day Challenge
Learn how pi is used by NASA and how many of its infinite digits have been calculated, then explore the science and engineering behind the 2024 Pi Day Challenge.
Update: March 15, 2024 – The answers to the 2024 NASA Pi Day Challenge are here! Take a peek at the illustrated answer key now available under each problem on the NASA Pi Day Challenge page.
This year marks the 11th installment of the NASA Pi Day Challenge. Celebrated on March 14, Pi Day is the annual holiday that pays tribute to the mathematical constant pi – the number that results from dividing any circle's circumference by its diameter.
Every year on March 14, Pi Day gives us a reason to enjoy our favorite sweet and savory pies and celebrate the mathematical wonder that helps NASA explore the universe. Students can join in the fun once again by using pi to explore Earth and space themselves with the NASA Pi Day Challenge.
Read on to learn more about the science behind this year's challenge and get students solving real problems faced by NASA scientists and engineers exploring Earth, the Moon, asteroids, and beyond!

Visit the Pi in the Sky 11 lesson page to explore classroom resources and downloads for the 2024 NASA Pi Day Challenge. Image credit: NASA/JPL-Caltech | + Expand image
What is Pi
Dividing any circle’s circumference by its diameter gives you an answer of pi, which is usually rounded to 3.14. Because pi is an irrational number, its decimal representation goes on forever and never repeats. In 2022, mathematician Simon Plouffe discovered the formula to calculate any single digit of pi. In the same year, teams around the world used cloud computing technology to calculate pi to 100 trillion digits. But you might be surprised to learn that for space exploration, NASA uses far fewer digits of pi.
Here at NASA, we use pi to map the Moon, measure Earth’s changing surface, receive laser-coded messages from deep space, and calculate asteroid orbits. But pi isn’t just used for exploring the cosmos. Since pi can be used to find the area or circumference of round objects and the volume or surface area of shapes like cylinders, cones, and spheres, it is useful in all sorts of ways. Transportation teams use pi when determining the size of new subway tunnels. Electricians can use pi when calculating the current or voltage passing through circuits. And you might even use pi to figure out how much fencing is needed around a circular school garden bed.
In the United States, March 14 can be written as 3.14, which is why that date was chosen for celebrating all things pi. In 2009, the U.S. House of Representatives passed a resolution officially designating March 14 as Pi Day and encouraging teachers and students to celebrate the day with activities that teach students about pi. And that's precisely what the NASA Pi Day Challenge is all about!
The Science Behind the 2024 NASA Pi Day Challenge
This 11th installment of the NASA Pi Day Challenge includes four illustrated math problems designed to get students thinking like scientists and engineers to calculate how to get a laser message to Earth, the change in an asteroid’s orbit, the amount of data that can be collected by an Earth satellite, and how a team of mini rovers will map portions of the Moon’s surface.
Read on to learn more about the science and engineering behind each problem or click the link below to jump right into the challenge.
› Take the NASA Pi Day Challenge
› Educators, get the lesson here!
Receiver Riddle
In December 2023, NASA tested a new way to communicate with distant spacecraft using technology called Deep Space Optical Communications, or DSOC. From 19,000,000 miles (30,199,000 km) away, the Psyche spacecraft beamed a high-definition video encoded in a near-infrared laser to Earth. The video, showing a cat named Taters chasing a laser, traveled at the speed of light, where it was received at Caltech’s Palomar Observatory. Because of the great distance the laser had to travel, the team needed to aim the transmission at where Earth would be when the signal arrived. In Receiver Riddle, use pi to determine where along Earth's orbit the team needed to aim the laser so that it could be received at the Observatory at the correct moment.
This animation shows how DSOC's laser signals are sent between the Psyche spacecraft and ground stations on Earth - first as a pointing reference to ensure accurate aiming of the narrow laser signal and then as a data transmission to the receiving station. Credit: NASA/JPL-Caltech/ASU| Watch on YouTube
Daring Deflection
In 2022, NASA crashed a spacecraft into the asteroid Dimorphos in an attempt to alter its orbit. The mission, known as the Double Asteroid Redirection Test, or DART, took place at an asteroid that posed no threat to our planet. Rather, it was an ideal target for NASA to test an important element of its planetary defense plan. DART was designed as a kinetic impactor, meaning it transferred its momentum and kinetic energy to Dimorphos upon impact, altering the asteroid's orbit. In Daring Deflection, use pi to determine the shape of Dimorphos’ orbit after DART crashed into it.

This image shows the final minutes of images leading up to the DART spacecraft's intentional collision with asteroid Dimorphos. Credit: NASA/Johns Hopkins APL | › Enlarge image
Orbit Observation
The NISAR mission is an Earth orbiting satellite designed to study our planet's changing ecosystems. It will collect data about Earth's land- and ice-covered surfaces approximately every 6 days, allowing scientists to study changes at the centimeter scale – an unprecedented level of detail. To achieve this feat, NISAR will collect massive amounts of data. In Orbit Observation, students use pi to calculate how much data the NISAR spacecraft captures during each orbit of Earth.

The NISAR satellite, shown in this artist’s concept, will use advanced radar imaging to provide an unprecedented view of changes to Earth’s land- and ice-covered surfaces. Credit: NASA/JPL-Caltech. | › Full image and caption
Moon Mappers
The CADRE project aims to land a team of mini rovers on the Moon in 2025 as a test of new exploration technology. Three suitcase-size rovers, each working mostly autonomously, will communicate with each other and a base station on their lunar lander to simultaneously measure data from different locations. If successful, the project could open the door for future multi-robot exploration missions. In Moon Mappers, students explore the Moon with pi by determining how far a CADRE rover drives on the Moon’s surface.

Engineers test the system that will lower three small rovers onto the lunar surface as part of the CADRE project. Credit: NASA/JPL-Caltech | › Full image and caption
Bring the Challenge Into the Classroom
Celebrate Pi Day by getting students thinking like NASA scientists and engineers to solve real-world problems in the NASA Pi Day Challenge. In addition to solving the 2024 challenge, you can also dig into the 40 puzzlers from previous challenges available in our Pi Day collection. Completing the problem set and reading about other ways NASA uses pi is a great way for students to see the importance of the M in STEM.
-
 Collection
CollectionEducator Guides – NASA Pi Day Challenge
Here's everything you need to bring the NASA Pi Day Challenge into the classroom.
Grades 4-12
Time Varies
-
 Student Activity
Student ActivityNASA Pi Day Challenge
The entire NASA Pi Day Challenge collection can be found in one, handy collection for students.
Grades 4-12
Time Varies
-

Downloads
Can't get enough pi? Download this year's NASA Pi Day Challenge graphics, including mobile phone and desktop backgrounds:
More Pi Resources
-
 Article
ArticleHow Many Decimals of Pi Do We Really Need?
While you may have memorized more than 70,000 digits of pi, world record holders, a JPL engineer explains why you really only need a tiny fraction of that for most calculations.
-
 Article
Article18 Ways NASA Uses Pi
Whether it's sending spacecraft to other planets, driving rovers on Mars, finding out what planets are made of or how deep alien oceans are, pi takes us far at NASA. Find out how pi helps us explore space.
- Article
10 Ways to Celebrate Pi Day With NASA on March 14
Find out what makes pi so special, how it’s used to explore space, and how you can join the celebration with resources from NASA.
-
 Infographic
InfographicPlanet Pi
This poster shows some of the ways NASA scientists and engineers use the mathematical constant pi (3.14) and includes common pi formulas.
-
 Article
Article18 Maneras en Que la NASA Usa Pi
Pi nos lleva lejos en la NASA. Estas son solo algunas de las formas en que pi nos ayuda a explorar el espacio.
Related Lessons for Educators
-
 Lesson
LessonCollisions in Space
Students predict and observe what happens when two objects collide to model collisions in space.
Grades K-4
Time 30 min to 1 hour
-
 Lesson
LessonMoon Phases
Students learn about the phases of the moon by acting them out.
Grades 1-6
Time 30 min to 1 hour
-
 Lesson
LessonModeling an Asteroid
Lead a discussion about asteroids and their physical properties, then have students mold their own asteroids out of clay.
Grades 3-5
Time 30 min to 1 hour
-
 Lesson
LessonMath Rocks: A Lesson in Asteroid Dynamics
Students use math to investigate a real-life asteroid impact.
Grades 8-12
Time 30 min to 1 hour
-
 Lesson
LessonModeling Crustal Folds
Students use playdough to model how Earth’s crust is bent and folded by tectonic plates over geologic time.
Grades 6-12
Time 30 min to 1 hour
-
 Lesson
LessonMaking Topographic Maps
Students draw and interpret topographic maps while learning about technology used to map Earth's surface, the seafloor, and other worlds.
Grades 6-12
Time 30 min to 1 hour
-
 Lesson
LessonCode a Radio Message for Space
Students code microcontrollers to send and receive radio signals, simulating communications between Earth and spacecraft.
Grades 6-12
Time 30 min to 1 hour
Related Activities for Students
-
 Student Project
Student ProjectDraw Your Own Psyche Spacecraft
Follow these easy instructions to draw and decorate your own model of the Psyche spacecraft.
Type Project
Subject Engineering
-
 Slideshow
SlideshowWhat's That Space Rock?
Find out how to tell the difference between asteroids, comets, meteors, meteorites and other bodies in our solar system.
Type Slideshow
Subject Science
Facts and Figures
Websites
Articles
- How NASA Studies and Tracks Asteroids Near and Far
- NASA Cat Video Explained
- Article for Kids: Asteroid or Meteor: What's the Difference?
- Article for Kids: What Is an Asteroid?
Videos
- The Video NASA’s Laser Communications Experiment Streamed From Deep Space
- NASA's DART Mission Confirms Crashing Spacecraft into Asteroids Can Deflect Them
Interactives
TAGS: Pi Day, Pi, Math, NASA Pi Day Challenge, moon, earth, asteroid, psyche, DART, CADRE, NISAR DSOC
Edu News | January 16, 2024
Doing the Math on Why We Have Leap Day
Leap day, Feb. 29, happens every four years because of a mismatch between the calendar year and Earth's orbit. Learn how it works, and get students engaged in leap day STEM.
You may have noticed that there's an extra day on your calendar this year. That's not a typo – it's leap day! Leap day is another name for Feb. 29, a date that typically comes around every four years, during a leap year.
Why doesn't Feb. 29 appear on the calendar every year?
The length of a year is based on how long it takes a planet to revolve around the Sun. Earth takes about 365.2422 days to make one revolution around the Sun. That's about six hours longer than the 365 days that we typically include in a calendar year. As a result, every four years, we have about 24 extra hours that we add to the calendar at the end of February in the form of leap day.
Without leap day, the dates of annual events, such as equinoxes and solstices, would slowly shift to later in the year, changing the dates of each season. After only a century without leap day, summer wouldn’t start until mid-July!
But the peculiar adjustments don't end there. If Earth revolved around the Sun in exactly 365 days and six hours, this system of adding a leap day every four years would need no exceptions. However, Earth takes a little less time than that to orbit the Sun. Rounding up and inserting a 24-hour leap day every four years adds about 45 extra minutes to every four-year leap cycle. That adds up to about three days every 400 years. To correct for that, years that are divisible by 100 don't have leap days unless they’re also divisible by 400.
If you do the math, you'll see that the year 2000 was a leap year, but 2100, 2200 and 2300 will not be.
Have students learn more about leap years with this article from NASA's Space Place, then have them do the math for themselves with this leap day problem set. You can also have students write a letter or poem to be opened on the next leap day or get them learning about orbits across the solar system.
And since we've got an extra 24 hours this year, don't forget to take a little time to relax!
Educator Resources
-
 Problem Set
Problem SetLeap Day Math
In this problem set, students calculate the difference between the calendar year and Earth's orbital period to determine when leap years occur.
Subject Math
Grades 5-8
Time Less than 30 mins
-
 Collection
CollectionSolar System Scale & Size Lessons
Explore a collection of standards-aligned lessons all about the size and scale of our solar system.
-
 Educator Guide
Educator GuidePlanetary Poetry
Have students write a poem they can open and re-read next leap day!
Subject Science
Grades 2-12
Time 1-2 hrs
Student Resources
-
 Article
ArticleWhat Is a Leap Year?
Get the answer in this article from NASA Space Place. Plus, learn if other planets have leap years!
-
 Article
ArticleHow Long Is a Year on Other Planets?
Get the answer in this article from NASA Space Place.
-
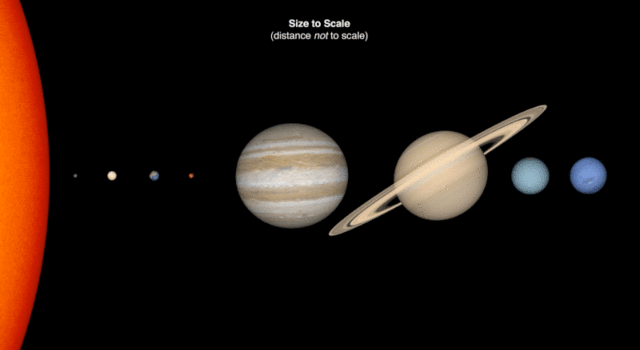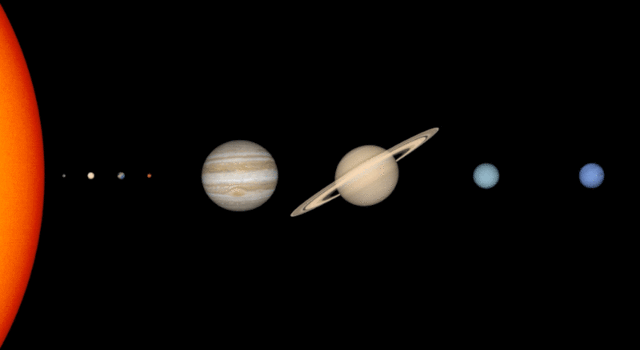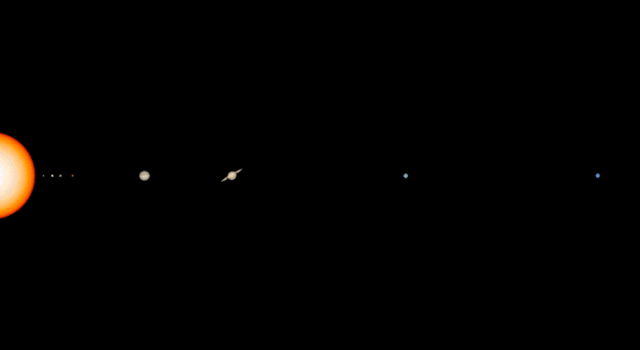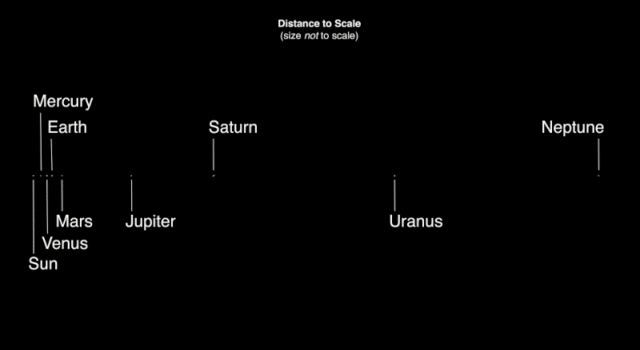 Collection
CollectionAll About the Size and Scale of the Solar System
Learn how big and far away the planets are with these projects and activities.
TAGS: K-12 Education, Math, Leap Day, Leap Year, Events, Space, Educators, Teachers, Parents, Students, STEM, Lessons, Earth Science, Earth
Teachable Moments | November 27, 2023
NASA Balloon Mission Designed to See the Space Between Stars
Get to know GUSTO and learn how to bring the science and engineering behind this unique balloon-based mission into the classroom.
A NASA balloon mission designed to study the interstellar medium – the space between stars – will take to the skies above Antarctica in December 2023.
Read on to learn how the GUSTO mission's unique design and science goals can serve as real-life examples of STEM concepts. Then, explore lessons and resources you can use to get students learning more.
What the GUSTO Mission Will Do
Though many people think of space as empty except for things like stars, planets, moons, asteroids, meteors, and comets, it’s anything but. Typically, there is one molecule of matter in every cubic centimeter of the space between stars known as the interstellar medium. In more dense clouds of interstellar gas, there could be as many as 1,000,000 molecules per cubic centimeter. It might not seem like much compared with the 10,000,000,000,000,000,000 molecules in every cubic centimeter of air we breathe, but the interstellar medium can tell us a lot about how stars and planets form and what role gases and dust play in our galaxy and others.

This diagram shows the life cycles of Sun-like and massive stars. Credit: NASA, Night Sky Network | › Learn more about star life cycles
Like plants and animals, stars have a life cycle that scientists want to better understand. Gases and dust grains that make up a dense interstellar cloud, known as a nebula, can become disturbed, and under the pull of their own gravity, begin collapsing in on themselves. Eventually stars form from the gas and planets form from the dust. As a star goes through its life, it eventually runs out of sources of energy. When this happens, the star dies, expelling gases – sometimes violently, as in a supernova – into a new gas cloud. From here, the cycle can start again. Scientists want to know more about the many factors at play in this cycle. This is where GUSTO comes in.
GUSTO – short for Galactic/Extragalactic ULDB Spectroscopic Terahertz Observatory – is a balloon-based telescope that will study the interstellar medium, the small amount of gas and dust between the stars. From its vantage point high above almost all of the Earth’s atmosphere, GUSTO will measure carbon, nitrogen, and oxygen emissions in the far-infrared portion of the electromagnetic spectrum, focusing its sights on the Milky Way galaxy and the nearby galaxy known as the Large Magellanic Cloud.

Our galaxy, the Milky Way, has hundreds of billions of stars and enough gas and dust to make billions more stars. Credit: NASA | › Full image and caption
The mission is designed to provide scientists with data that will help them understand the complete lifecycle of the gas and dust that forms planets and stars. To achieve its goals, GUSTO will study:
- The composition and formation of molecular clouds in these regions.
- The formation, birth, and evolution of stars from molecular clouds.
- The formation of gas clouds following the deaths of stars. And the re-start of this cycle.

Nearly 200,000 light-years from Earth, the Large Magellanic Cloud is a satellite galaxy of the Milky Way. Vast clouds of gas within it slowly collapse to form new stars. In turn, these light up the gas clouds in a riot of colors, visible in this image from the Hubble Space Telescope. Credit: NASA | › Full image and caption
Scientists hope to use the information collected by GUSTO to develop models of the Milky Way and Large Magellanic Cloud. Studying these two galaxies allows scientists to observe more details and make more accurate models. Those models can then be used for comparing and studying more distant galaxies that are harder to observe.
Why Fly on a Balloon?
Unlike most NASA missions, GUSTO won’t launch on a rocket. It will be carried to approximately 120,000 feet (36.5 kilometers) above Antarctica using what’s known as a Long Duration Balloon, or LDB.
Balloon missions provide a number of advantages to scientists conducting research. They are more affordable than missions that go to space and require less time to develop. They also offer a way to test new scientific instruments and technologies before they are used in space. For these reasons, balloons have become a popular way for university students to gain experience building and testing science instruments.
Explore how balloons are being used for Earth and space science in this video from the Johns Hopkins Applied Physics Laboratory, which is providing the mission operations for GUSTO and the balloon gondola where the mission's instruments will be mounted. | Watch on YouTube
GUSTO's use of the Long Duration Balloon provided by NASA’s Balloon Science Program offers several advantages over other types of scientific balloons. Conventional scientific balloons stay aloft for a few hours or a few days and rely on the balloon maintaining a line-of-sight to send and receive data. Long Duration Balloons use satellites for sending data and receiving commands and can stay afloat for a few weeks to a couple of months.
Made with a thin, strong, plastic film called polyethylene, LDBs are partially inflated with helium. As the balloon rises, the surrounding air pressure decreases, allowing the gas inside the balloon to expand, increasing the volume and pressure of the balloon. When fully expanded, the balloon has a volume of around 40 million cubic feet (1.1 million cubic meters). That’s big enough to fit an entire football stadium inside.

GUSTO will be attached to a balloon gondola like the one depicted in this artist's rendering. | + Expand image
The telescope itself will be attached to a platform known as a gondola, which is home to several components that make the mission possible. The multi-axis control system will keep the platform stable during flight, allowing for precisely pointing GUSTO’s 35-inch (90-centimeter) diameter telescope in the right direction. Cryocoolers and liquid helium will keep the telescope’s scientific instruments at the necessary low temperature of -452°F (4° Kelvin). And the gondola will house a radio system that allows operators on the surface to control the balloon and telescope. All these systems will be powered by lithium-ion batteries charged during flight by a set of solar arrays.
Location is Everything
GUSTO is designed to measure terahertz wavelengths (in the far-infrared portion of the electromagnetic spectrum), a range of energy that is easily absorbed by water vapor. However, the observatory's altitude will put it in the upper half of the stratosphere and above 99% of the water vapor in the atmosphere. This makes it an ideal location for the mission to make its measurements and avoid factors that might otherwise obstruct its view.

GUSTO will make its observations from the upper half of the stratosphere, which offers several benefits over observing from lower in the atmosphere or from the ground. Credit: NASA | › Explore the interactive graphic
The stratosphere offers another advantage for GUSTO. This layer of the atmosphere warms as altitude increases, making the top of the stratosphere warmer than the bottom. The colder air at the bottom and warmer air at the top prevents mixing and air turbulence, making the air very stable and providing a great place to observe space. You may have noticed this stability if you’ve seen a flat-topped anvil-shaped storm cloud. That flat top is the cloud reaching the bottom of the stratosphere, where the stable air prevents the cloud from mixing upward.
But why fly GUSTO above Antarctica? Even though balloons can be launched from all over the planet, the 24 hours of sunlight per day provided by the Antarctic summer make the south polar region an ideal launch location for a solar-powered mission like GUSTO. But more important is a weather phenomenon known as an anticyclone. This weather system is an upper-atmosphere counter-clockwise wind flow that circles the South Pole about every two weeks. The Antarctic anticyclone allows for long balloon flights of missions that can be recovered and potentially reflown.
Preparing for Liftoff
To launch a balloon mission in Antarctica, weather conditions have to be just right. The anticyclone typically forms in mid-December but can arrive a little earlier or a little later. Even with the anticyclone started, winds on the ground and in the first few hundred feet of the atmosphere need to be under six knots (seven miles per hour) for GUSTO to launch. A NASA meteorologist provides daily updates on the cyclone and the ground.
Once weather conditions are good and the balloon is launched, it will circle Antarctica about once every 14 days with the wind. The anticyclone typically lasts one to two months. Because GUSTO may be in the air for more than two months, it’s possible that the mission will continue after the anticyclone ends, causing the balloon to drift northward as winter progresses.
Bring GUSTO Into the Classroom
The GUSTO mission is a great opportunity to engage students with hands-on learning opportunities. Students can build a planetary exploration balloon and model how interstellar dust forms into planets. Explore these lessons and resources to get students excited about the STEM involved in the mission.
Resources for Educators
-
 Lesson
LessonMake a Planetary Exploration Balloon
In this engineering challenge, students must stay within design limitations while creating a balloon and gondola system that can descend or ascend at a given rate or maintain its altitude.
Subject Science
Grades 3-12
Time Less than 30 mins
-
 Lesson
LessonThe Science of Color
Quickly and easily model how colors reflect, absorb, and interact with each other in the classroom or online using your computer’s camera.
Subject Science
Grades 2-8
Time 30-60 mins
-
 Interactive
InteractiveStar Formation: Eagle Nebula
View the Eagle Nebula in different wavelengths to see how new details emerge.
Subject Science
Resources for Students
-
 Project
ProjectMake a Planetary Exploration Balloon
Find out how NASA uses balloons to explore Earth and space and then take on a challenge to design your own balloon explorer inspired by what you've learned!
Subject Science
Grades 3-12
Time 30-60 mins
-
 Article
ArticleWhat Is a Galaxy?
Learn what galaxies are made of in this article from NASA Space Place.
-
 Article
ArticleHow Old Are Galaxies?
Get the answer in this article from NASA Space Place.
-
 Interactive
InteractiveExplore the Electromagnetic Spectrum
Click through this interactive from NASA Space Place all about the electromagnetic spectrum.
NASA's Universe of Learning materials are based upon work supported by NASA under award number NNX16AC65A to the Space Telescope Science Institute, working in partnership with Caltech/IPAC, Center for Astrophysics | Harvard & Smithsonian, and the Jet Propulsion Laboratory.
TAGS: GUSTO, Astronomy, Astrophysics, Science, Teaching, Learning, K-12, Classroom, Teachable Moments, Universe of Learning, Balloon Mission, Missions
Teachable Moments | April 28, 2023
May the Force = mass x acceleration
Science fiction meets science fact in this Star Wars inspired Teachable Moment all about ion propulsion and Newton’s Laws.
In the News
What do "Star Wars," NASA's Dawn spacecraft and Newton's Laws of Motion have in common? An educational lesson that turns science fiction into science fact using spreadsheets – a powerful tool for developing the scientific models addressed in the Next Generation Science Standards. Keep reading to learn more and find out how to get students wielding the force.
Why It's Important
The TIE (Twin Ion Engine) fighter is a staple of the "Star Wars" universe. Darth Vader flew one in "A New Hope." Poe Dameron piloted one in "The Force Awakens." And many, many Imperial pilots met their fates in them. While the fictional TIE fighters in "Star Wars" flew a long time ago in a galaxy far, far away, ion engines are a reality in this galaxy today – and have a unique connection to NASA’s Jet Propulsion Laboratory.
Launched in 1998, the first spacecraft to use an ion engine was Deep Space 1, which flew by asteroid 9969 Braille and comet Borrelly. Fueled by the success of Deep Space 1, engineers at JPL set forth to develop the next spacecraft that would use ion propulsion. This mission, called Dawn, would take ion-powered spacecraft to the next level by allowing Dawn to go into orbit twice – around the two largest objects in the asteroid belt: Vesta and Ceres.
How It Works
Ion engines rely on two principles that Isaac Newton first described in 1687. First, a positively charged atom (ion) is pushed out of the engine at a high velocity. Newton’s Third Law of Motion states that for every action there is an equal and opposite reaction, so then a small force pushes back on the spacecraft in the opposite direction – forward! According to Newton’s Second Law of Motion, there is a relationship between the force (F) exerted on an object, its mass (m) and its acceleration (a). The equation F=ma describes that relationship and tells us that the small force applied to the spacecraft by the exiting atom provides a small amount of acceleration to the spacecraft. Push enough atoms out, and you'll get enough acceleration to really speed things up.
Why is It Important?
Compared with traditional chemical rockets, ion propulsion is faster, cheaper and safer:
- Faster: Spacecraft powered by ion engines can reach speeds of up to 90,000 meters per second (more than 201,000 mph!)
- Cheaper: When it comes to fuel efficiency, ion engines can reach more than 90 percent fuel efficiency, while chemical rockets are only about 35 percent efficient.
- Safer: Ion thrusters are fueled by inert gases. Most of them use xenon, which is a non-toxic, chemically inert (no risk of exploding), odorless, tasteless and colorless gas.
These properties make ion propulsion a very attractive solution when engineers are designing spacecraft. While not every spacecraft can use ion propulsion – some need greater rates of acceleration than ion propulsion can provide – the number and types of missions using these efficient engines is growing. In addition to being used on the Dawn spacecraft and communication satellites orbiting Earth, ion propulsion could be used to boost the International Space Station into higher orbits and will likely be a part of many future missions exploring our own solar system.
Teach It
Newton’s Laws of Motion are an important part of middle and high school physical science and are addressed specifically by the Next Generation Science Standards as well as Common Core Math standards. The lesson "Ion Propulsion: Using Spreadsheets to Model Additive Velocity" lets students study the relationship between force, mass and acceleration as described by Newton's Second Law as they develop spreadsheet models that apply those principles to real-world situations.
Educator Guides
-

Using Spreadsheets to Model Additive Velocity
Students develop spreadsheet models that describe the relationship between the mass of a spacecraft, the force acting on the craft, and its acceleration.
Grades 6-12
Time 30-60 mins
-

Motion and Forces Lessons
Get students wielding "the force" with these standards-aligned lessons all about motion and forces.
Grades K-12
Time Varies
Student Activities
Explore More
- Website: Dawn Mission
- Blog: Dawn Journal
- Video: Crazy Engineering - Ion Propulsion
- Ion propulsion interactives
- Eyes on the Solar System: Dawn Mission Tour (scroll to "Solar System Tours" and click the "Dawn" link)
This feature was originally published on May 3, 2016.
TAGS: May the Fourth, Star Wars Day, F=ma, ion propulsion, Dawn, Deep Space 1, lesson, classroom activity, NGSS, Common Core Math
Teachable Moments | March 9, 2023
10 Years of NASA's Pi Day Challenge
Learn how pi is used by NASA and how many of its infinite digits have been calculated, then explore the science and engineering that makes the Pi Day Challenge possible.
Update: March 15, 2023 – The answers are here! Visit the NASA Pi Day Challenge page to view the illustrated answer keys for each problem.
This year marks the 10th installment of the NASA Pi Day Challenge. Celebrated on March 14, Pi Day is the annual holiday that pays tribute to the mathematical constant pi – the number that results from dividing any circle's circumference by its diameter.
Every year, Pi Day gives us a reason to celebrate the mathematical wonder that helps NASA explore the universe and enjoy our favorite sweet and savory pies. Students can join in the fun once again by using pi to explore Earth and space themselves in the NASA Pi Day Challenge.
Read on to learn more about the science behind this year's challenge and find out how students can put their math mettle to the test to solve real problems faced by NASA scientists and engineers as we explore Earth, Mars, asteroids, and beyond!

Visit the Pi in the Sky 10 lesson page to explore classroom resources and downloads for the 2023 NASA Pi Day Challenge. Image credit: NASA/JPL-Caltech | + Expand image

This illustration shows a concept for multiple robots that would team up to ferry to Earth samples of rocks and soil being collected from the Martian surface by NASA's Mars Perseverance rover. Image credit: NASA/JPL-Caltech | › Full image and caption

Image from animation comparing the relative sizes of James Webb's primary mirror to Hubble's primary mirror. Credit: NASA/Goddard Space Flight Center . | › Full animation

This illustration depicts the metal-rich asteroid Psyche, which is located in the main asteroid belt between Mars and Jupiter. Credits: NASA/JPL-Caltech/ASU | + Full image and caption

This image sequence shows an annular solar eclipse from May 2012. The bottom right frame illustrates the distinctive ring, or "annulus," of such eclipses. A similar eclipse will be visible from the South Pacific on May 10, 2013. Credits: Brocken Inaglory, CC BY-SA 3.0, via Wikimedia Commons | + Expand image
How It Works
Dividing any circle’s circumference by its diameter gives you an answer of pi, which is usually rounded to 3.14. Because pi is an irrational number, its decimal representation goes on forever and never repeats. In 2022, mathematician Simon Plouffe discovered the formula to calculate any single digit of pi. In the same year, teams around the world used cloud computing technology to calculate pi to 100 trillion digits. But you might be surprised to learn that for space exploration, NASA uses far fewer digits of pi.
Here at NASA, we use pi to measure the area of telescope mirrors, determine the composition of asteroids, and calculate the volume of rock samples. But pi isn’t just used for exploring the cosmos. Since pi can be used to find the area or circumference of round objects and the volume or surface area of shapes like cylinders, cones, and spheres, it is useful in all sorts of ways. Transportation teams use pi when determining the size of new subway tunnels. Electricians can use pi when calculating the current or voltage passing through circuits. And you might even use pi to figure out how much fencing is needed around a circular school garden bed.
In the United States, March 14 can be written as 3.14, which is why that date was chosen for celebrating all things pi. In 2009, the U.S. House of Representatives passed a resolution officially designating March 14 as Pi Day and encouraging teachers and students to celebrate the day with activities that teach students about pi. And that's precisely what the NASA Pi Day Challenge is all about!
The Science Behind the 2023 NASA Pi Day Challenge
This 10th installment of the NASA Pi Day Challenge includes four noodle-nudgers that get students using pi to calculate the amount of rock sampled by the Perseverance Mars rover, the light-collecting power of the James Webb Space Telescope, the composition of asteroid (16) Psyche, and the type of solar eclipse we can expect in October.
Read on to learn more about the science and engineering behind each problem or click the link below to jump right into the challenge.
› Take the NASA Pi Day Challenge
› Educators, get the lesson here!
Tubular Tally
NASA’s Mars rover, Perseverance, was designed to collect rock samples that will eventually be brought to Earth by a future mission. Sending objects from Mars to Earth is very difficult and something we've never done before. To keep the rock cores pristine on the journey to Earth, the rover hermetically seals them inside a specially designed sample tube. Once the samples are brought to Earth, scientists will be able to study them more closely with equipment that is too large to make the trip to Mars. In Tubular Tally, students use pi to determine the volume of a rock sample collected in a single tube.
Rad Reflection
When NASA launched the Hubble Space Telescope in 1990, scientists hoped that the telescope, with its large mirror and sensitivity to ultraviolet, visible, and near-infrared light, would unlock secrets of the universe from an orbit high above the atmosphere. Indeed, their hope became reality. Hubble’s discoveries, which are made possible in part by its mirror, rewrote astronomy textbooks. In 2022, the next great observatory, the James Webb Space Telescope, began exploring the infrared universe with an even larger mirror from a location beyond the orbit of the Moon. In Rad Reflection, students use pi to gain a new understanding of our ability to peer deep into the cosmos by comparing the area of Hubble’s primary mirror with the one on Webb.
Metal Math
Orbiting the Sun between Mars and Jupiter, the asteroid (16) Psyche is of particular interest to scientists because its surface may be metallic. Earth and other terrestrial planets have metal cores, but they are buried deep inside the planets, so they are difficult to study. By sending a spacecraft to study Psyche up close, scientists hope to learn more about terrestrial planet cores and our solar system’s history. That's where NASA's Psyche comes in. The mission will use specialized tools to study Psyche's composition from orbit. Determining how much metal exists on the asteroid is one of the key objectives of the mission. In Metal Math, students will do their own investigation of the asteroid's makeup, using pi to calculate the approximate density of Psyche and compare that to the density of known terrestrial materials.
Eclipsing Enigma
On Oct. 14, 2023, a solar eclipse will be visible across North and South America, as the Moon passes between Earth and the Sun, blocking the Sun's light from our perspective. Because Earth’s orbit around the Sun and the Moon’s orbit around Earth are not perfect circles, the distances between them change throughout their orbits. Depending on those distances, the Sun's disk area might be fully or only partially blocked during a solar eclipse. In Eclipsing Enigma, students get a sneak peek at what to expect in October by using pi to determine how much of the Sun’s disk will be eclipsed by the Moon and whether to expect a total or annular eclipse.
Teach It
Celebrate Pi Day by getting students thinking like NASA scientists and engineers to solve real-world problems in the NASA Pi Day Challenge. In addition to solving this year’s challenge, you can also dig into the more than 30 puzzlers from previous challenges available in our Pi Day collection. Completing the problem set and reading about other ways NASA uses pi is a great way for students to see the importance of the M in STEM.
Pi Day Resources
-

Pi in the Sky Lessons
Here's everything you need to bring the NASA Pi Day Challenge into the classroom.
Grades 4-12
Time Varies
-

NASA Pi Day Challenge
The entire NASA Pi Day Challenge collection can be found in one, handy slideshow for students.
Grades 4-12
Time Varies
-

How Many Decimals of Pi Do We Really Need?
While you may have memorized more than 70,000 digits of pi, world record holders, a JPL engineer explains why you really only need a tiny fraction of that for most calculations.
-

18 Ways NASA Uses Pi
Whether it's sending spacecraft to other planets, driving rovers on Mars, finding out what planets are made of or how deep alien oceans are, pi takes us far at NASA. Find out how pi helps us explore space.
-
10 Ways to Celebrate Pi Day With NASA on March 14
Find out what makes pi so special, how it’s used to explore space, and how you can join the celebration with resources from NASA.
-

Infographic: Planet Pi
This poster shows some of the ways NASA scientists and engineers use the mathematical constant pi (3.14) and includes common pi formulas.
-

Downloads
Can't get enough pi? Download this year's NASA Pi Day Challenge graphics, including mobile phone and desktop backgrounds:
-

National Council of Teachers of Mathematics: Notice and Wonder
Creative brainstorming through noticing and wondering encourages student participation, engagement, and students' understanding of the NASA Pi Day Challenge.
Subject Mathematics
-
Pi Day: What's Going 'Round
Tell us what you're up to this Pi Day and share your stories and photos on our showcase page.
Plus, join the conversation using the hashtag #NASAPiDayChallenge on Facebook, Twitter, and Instagram.
Related Lessons for Educators
-

Robotic Arm Challenge
In this challenge, students will create a model robotic arm to move items from one location to another. They will engage in the engineering design process to design, build and operate the arm.
Grades K-8
Time 30 min to 1 hour
-

NASA's Mission to Mars Student Challenge
Take part in the exploration of Mars and bring students along for the ride with NASA's Perseverance rover.
Grades K-12
Time Varies
-

Moon Phases
Students learn about the phases of the moon by acting them out.
Grades 1-6
Time 30 min to 1 hour
-

Modeling the Earth-Moon System
Students learn about scale models and distance by creating a classroom-size Earth-Moon system.
Grades 6-8
Time 30 min to 1 hour
-

Math of the Expanding Universe
Students will learn about the expanding universe and the redshift of lightwaves, then perform their own calculations with a distant supernova.
Grades 9-12
Time 30 min to 1 hour
-
The Expanded Universe: Playing with Time Activity Guide
In this activity, participants use balloons to model the expansion of the universe and observe how expansion affects wavelengths of light and distance between galaxies
-

James Webb Space Telescope STEM Toolkit
Find a collection of resources, activities, videos, and more for your students to learn about NASA’s newest space observatory.
-

Modeling an Asteroid
Lead a discussion about asteroids and their physical properties, then have students mold their own asteroids out of clay.
Grades 3-5
Time 30 min to 1 hour
-

Math Rocks: A Lesson in Asteroid Dynamics
Students use math to investigate a real-life asteroid impact.
Grades 8-12
Time 30 min to 1 hour
Related Activities for Students
-

How to Make a Pinhole Camera
Learn how to make your very own pinhole camera to safely see a solar eclipse in action!
Type Project
Subject Engineering
-
Collection: Exploring Mars
Make a cardboard rover, design a Mars exploration video game and explore more STEM projects, slideshows and videos for students.
Type Project
Subject Science
-

What's That Space Rock?
Find out how to tell the difference between asteroids, comets, meteors, meteorites and other bodies in our solar system.
Type Slideshow
Subject Science
-

10 Things We Can Learn from Webb's First Images
Take a closer look at how images from NASA's most powerful space telescope yet are helping to answer some of astronomers' most burning questions.
Type Slideshow
Subject Science
Recursos en español
Facts and Figures
Websites
- Webb Space Telescope
- Mars Exploration
- Perseverance Mars Rover
- Mars Sample Return
- Psyche Mission
- MIRI Instrument
- 2023 Eclipse
Articles
Videos
Interactives
TAGS: Pi Day, Pi, Math, NASA Pi Day Challenge, sun, moon, earth, eclipse, asteroid, psyche, sample return, mars, perseverance, jwst, webb, hubble, telescope, miri
Teachable Moments | January 3, 2023
How InSight Revealed the Heart of Mars
As NASA retires its InSight Mars lander, here's a look at some of the biggest discoveries from the first mission designed to study the Red Planet's interior – plus, how to make connections to what students are learning now.
After more than four years listening to the “heartbeat” of Mars, NASA is saying goodbye to the InSight lander as the mission on the Red Planet comes to an end. On Dec. 21, 2022 scientists wrapped up the first-of-its-kind mission to study the interior of Mars as dust in the Martian atmosphere and on the spacecraft’s solar panels prevented the lander from generating enough power to continue.
Read on to learn how the mission worked, what it discovered, and how to bring the science and engineering of the mission into the classroom.
How It Worked

The locations of InSight's three main science tools, SEIS, HP3, and RISE are labeled in this illustration of the lander on Mars. | + Expand image | › Full image and caption
The InSight lander was designed to reveal the processes that led to the formation of Mars – as well as Earth, the Moon, and all rocky worlds. This meant meeting two main science goals.
First, scientists wanted to understand how Mars formed and evolved. To do that, they needed to investigate the size and make-up of Mars’ core, the thickness and structure of its crust, the structure of the mantle layer, the warmth of the planet's interior, and the amount of heat flowing through the planet.
Second, to study tectonic activity on Mars, scientists needed to determine the power, frequency, and location of “marsquakes” as well as measure how often meteoroids impacted the Red Planet, creating seismic waves.
Engineers equipped InSight with three main science tools that would allow researchers to answer these questions about Mars.
SEIS, a seismometer like the ones used on Earth to record earthquakes, measured the seismic waves on Mars. These waves, which travel through the Red Planet, can tell scientists a lot about the areas they pass through. They even carry clues about whether it was a marsquake or meteorite impact that created the waves.

InSight captured these images of clouds drifting in the distance, visible just beyond the dome-like top of the SEIS instrument. Credit: NASA/JPL-Caltech | + Expand image | › Full image and caption
InSight's Heat Flow and Physical Properties Package, or HP3, was an instrument designed to burrow 16 feet (five meters) into Mars to measure the temperature at different depths and monitor how heat flowed out toward the surface. However, the self-hammering probe, informally called the "mole," struggled to dig itself in due to the unexpected consistency of the top few inches of Mars regolith at the landing site. Using full-size models of the lander and probe, engineers recreated InSight’s environment here on Earth to see if they could find a solution to the issue. They tested solutions that would allow the probe to penetrate the surface, including pressing the scoop attached to InSight’s robotic arm against the probe. While the effort serves as a great real-world example of how engineers work through problems with distant spacecraft, ultimately, none of the solutions allowed the probe to dig past the surface when attempted on Mars.
In 2019, InSight mission scientist/engineer Troy Hudson shared the game plan for getting the mission's heat probe digging again on Mars. Ultimately, the team wasn't able to to get the "mole" working, but the effort is a great real-world example of how engineers work through problems with distant spacecraft. | Watch on YouTube
InSight’s third experiment, called RISE, used the spacecraft’s radio antennas to precisely measure the lander's position on the surface of Mars. The interior structure of Mars affects the planet’s motion, causing it to wobble. Measuring InSight’s position as the planet wobbled helped scientists gain a better understanding of the core and other layered structures that exist within the interior of Mars.
What We Discovered

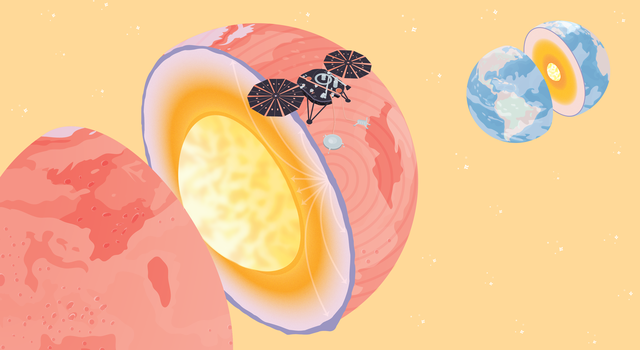
Using its seismometer, InSight gained a deeper understanding of the interior layers of Mars, as detailed in this graphic. Image credit: NASA/JPL-Caltech | + Expand image | › Full image and caption
InSight’s instruments enabled the mission science team to gain an understanding of not only the depth of Mars’ crust, mantle, and core, but also the composition of those features. They also learned just how active Mars really is.
The Structure of Mars
Working our way from the surface to the center of the planet, scientists found Mars’ crust was thinner than expected. Seismic waves detected by SEIS indicate that the crust is made up of three sub-layers, similar to Earth’s crust. The top-most layer of the crust is about six miles (10 kilometers) deep, while the denser layers of the crust, which contain more felsic, or iron-rich, material extend downward to about 25 miles (40 kilometers) below the surface. As seismic waves from a marsquake or a meteorite impact spread across the surface and through the interior of the planet, they can reflect off of underground layers, giving scientists views into the unseen materials below. Measuring how the waves change as a result of these reflections is how scientists unveiled the underground structure of Mars.
Like Earth, Mars has a lithosphere, a rigid layer made up of the crust and upper mantle. The Martian lithosphere extends about 310 miles (500 kilometers) below the surface before it transitions into the remaining mantle layer, which is relatively cool compared with Earth’s mantle. Mars’ mantle extends to 969 miles (1,560 kilometers) below the surface where it meets the planet’s core.

In this lesson from the "Pi in the Sky" math challenge, students use measurements from InSight along with pi to calculate the density of Mars' core. Image credit: NASA/JPL-Caltech | + Expand image | › Go to the lesson
Scientists measured the core of Mars and found it to be larger than expected, with a radius of 1,137 miles (1,830 kilometers). With this information, scientists were able to estimate the density of Mars' core, which turned out to be less dense than anticipated, meaning it contains lighter elements mixed in with iron. Scientists also confirmed that the planet contains a liquid core. While we know that Earth has a liquid outer core and solid inner core, scientists will need to further study the data returned from InSight to know if there is also a solid inner core on Mars.
As scientists continue to study the data returned from InSight, we could learn even more about how Mars formed, how its magnetic field developed, and what materials make up the core, which could ultimately help us better understand how Earth and other planets formed.
Marsquakes
InSight discovered that Mars is a very active planet. A total of 1,319 marsquakes were detected after the SEIS instrument was placed on the surface. The largest, which was estimated to be a magnitude 5, was detected in May of 2022.
Unlike Earth, where the crust is broken into large pieces called plates that continually shift around causing earthquakes, Mars’ crust is made up of one solid plate, somewhat like a shell. However, as the planet cools, the crust shrinks, creating breaks called faults. This breaking action is what causes marsquakes, and the seismic waves generated by the quakes are what help scientists figure out when and where the quakes occurred and how powerful they were.

In this math problem from the "Pi in the Sky" series, students use pi to identify the timing and location of a hypothetical marsquake recorded by InSight. Image credit: NASA/JPL-Caltech | + Expand image | › Go to the lesson
Nearly all of the strongest marsquakes detected by InSight came from a region known as Cerberus Fossae, a volcanic region that may have had lava flows within the past few million years. Volcanic activity, even without lava flowing on the surface, can be another way marsquakes occur. Images from orbiting spacecraft show boulders that have fallen from cliffs in this region, perhaps shaken loose by large marsquakes.

This seismogram shows the largest quake ever detected on another planet. Estimated at magnitude 5, this quake was discovered by InSight on May 4, 2022. Listen to a sonification of this seismogram. | + Expand image | › Full image and caption
Conversely, InSight didn't detect any quakes in the volcanic region known as Tharsis, the home of three of Mars’ largest volcanos that sit approximately one-third of the way around the planet from InSight. This doesn’t necessarily mean the area is not seismically active. Scientists think there may be quakes occurring, but the size of Mars’ liquid core creates what’s known as a shadow zone – an area into which seismic waves don’t pass – at InSight's location.
Meteorite Impacts
On Sept. 5, 2021, InSight detected the impacts of a meteoroid that entered the Martian atmosphere. The meteoroid exploded into at least three pieces that reached the surface and left behind craters. NASA’s Mars Reconnaissance Orbiter passed over the impact sites to capture images of the three new craters and confirm their locations.

This image, captured by the Mars Reconnaissance Orbiter, shows the craters (in blue) formed by a meteroid impact on Mars on Sept. 5, 2021. The impact was the first to be detected by InSight. Image credit: NASA/JPL-Caltech/University of Arizona | + Expand image | › Full image and caption
“After three years of waiting for an impact, those craters looked beautiful,” said Ingrid Daubar of Brown University, a Mars impacts specialist.
Mars’ thin atmosphere, which is less than 1% as dense as Earth’s, means meteoroids have a better chance of not disintegrating in the heat and pressure that builds up as they pass through the atmosphere to the planet’s surface. Despite this fact and Mars' proximity to the asteroid belt, the planet proved to be a challenging location to detect meteorite impacts because of "noise" in the data created by winds blowing on SEIS and seasonal changes in the atmosphere.
With the confirmation of the September 2021 impacts, scientists were able to identify a telltale seismic signature to these meteorite impacts. With this information in hand, they looked back through InSight's data and found three more impacts – one in 2020 and two in 2021. Scientists anticipate finding even more impacts in the existing data that might have been hidden by the noise in the data.

This collage shows three other meteoroid impacts on Mars that were detected by the seismometer on InSight and captured by the Mars Reconnaissance Orbiter. Image credit: Credit: NASA/JPL-Caltech/University of Arizona | + Expand image | › Full image and caption
Meteorite impacts are an invaluable piece of understanding the planet’s surface. On a planet like Earth, wind, rain, snow and ice wear down surface features in a process known as weathering. Plate tectonics and active volcanism refresh Earth’s surface regularly. Mars’ surface is older and doesn't go through those same processes, so a record of past geologic events like meteorite impacts is more apparent on the planet's surface. By counting impact craters visible on Mars today, scientists can update their models and better estimate the number of impacts that occurred in the early solar system. This gives them an improved approximation of the age of the planet’s surface.
Learn how InSight detected the first seismic waves from a meteoroid on Mars and how the lander captured the sound of the space rock striking the surface. | Watch on YouTube
Why It's Important
Before InSight touched down, all Mars missions – landers, rovers, orbiters and flyby spacecraft – studied the surface and atmosphere of the planet. InSight was the first mission to study the deep interior of Mars.
Even with the InSight mission drawing to a close, the science and engineering of the mission will continue to inform our understanding of the Red Planet and our solar system for years as researchers further examine the data returned to Earth. Keep up to date with the latest findings from InSight scientists and engineers on the mission website.
Teach It
Explore these lessons in geology, physics, math, coding and engineering to connect student learning to the InSight mission and the real-world STEM that happens at NASA.
Educator Resources
-
 Collection
CollectionInSight Lessons for Educators
Explore a collection of standards-aligned lessons to bring the science and engineering of the InSight mission into the classroom.
-
 Collection
CollectionNASA's Mission to Mars Student Challenge
Get K-12 students exploring Mars with NASA scientists, engineers, and the Perseverance rover as they learn all about STEM and design their very own mission to the Red Planet!
-
 Teachable Moments
Teachable MomentsNASA InSight Lander to Get First Look at ‘Heart’ of Mars
Learn what it takes to travel to Mars and get students engaged with lessons in calculating trajectories, plus building and launching rockets.
-
 Teachable Moments
Teachable MomentsMars Landing to Deliver Science Firsts
Find out how NASA’s InSight lander will collect all-new science at Mars, then get students doing similar investigations in the classroom.
Student Activities
Explore More
- Website: Mars InSight Mission
- Podcast: On a Mission - Season 1
- Articles: JPL News - InSight Mission
- Videos: InSight Mission Videos
- Images: InSight Mission Images
- Video: Interns Explore the Future at NASA-JPL
- Videos: Inside InSight - YouTube Playlist
- Videos: InSight Mission to Mars - YouTube Playlist
- Interactive: Experience InSight
- Website: NASA Mars Exploration
- Articles: People - Meet the Martians
- Resources for Kids: Space Place - All About Mars
TAGS: K-12 Education, Classrooms, Teaching, Teachers, Resources, Teachable Moments, Mars, InSight, Missions, Spacecraft, Marsquakes
Teachable Moments | October 20, 2022
The Science Behind NASA's First Attempt at Redirecting an Asteroid
Find out more about the historic first test, which could be used to defend our planet if a hazardous asteroid were discovered. Plus, explore lessons to bring the science and engineering of the mission into the classroom.
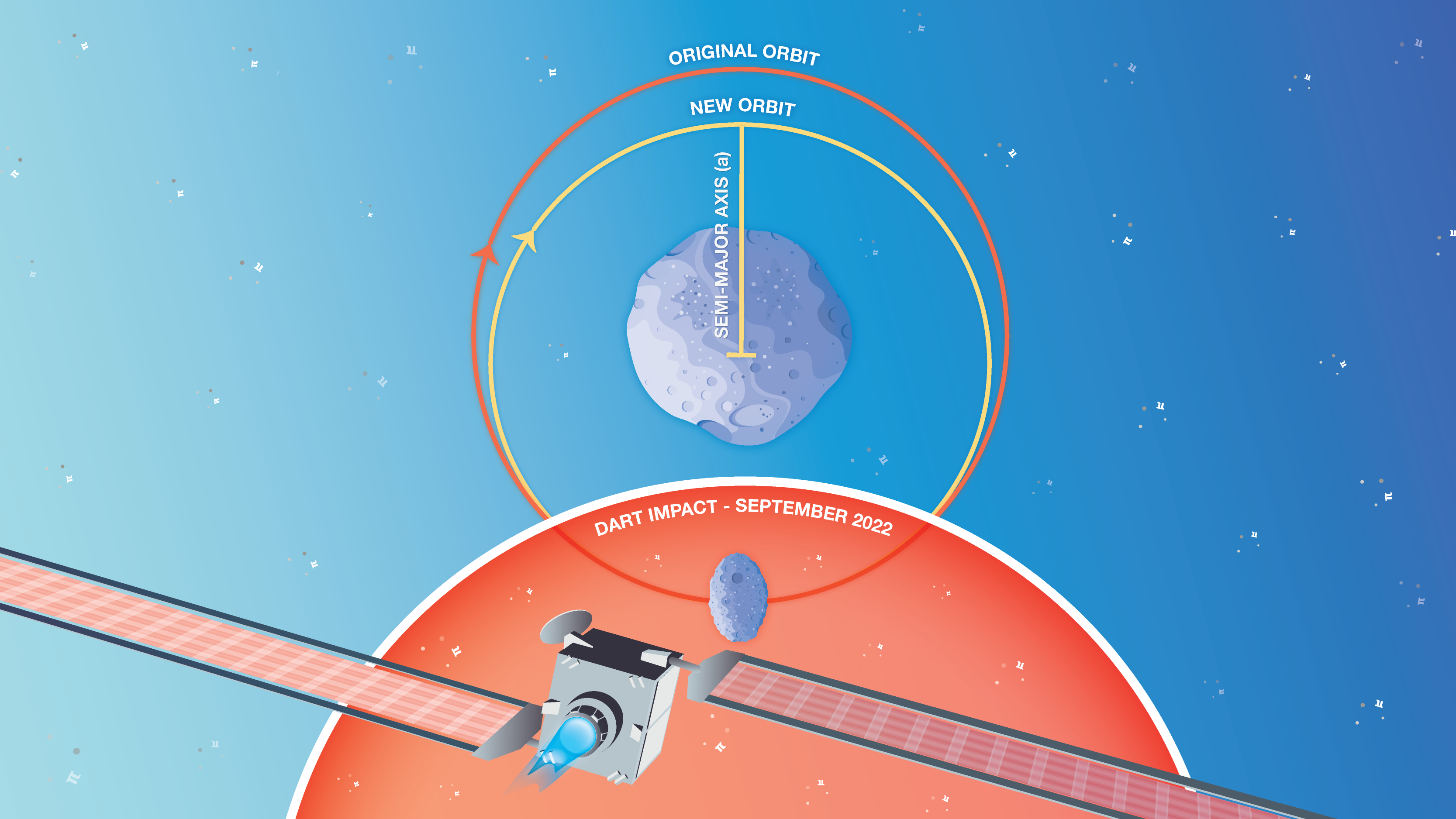
Update: Oct. 20, 2022 – The DART spacecraft successfully impacted the asteroid Dimorphos on September 26, reducing the period of the asteroid's orbit by 32 minutes. Scientists considered a change of 73 seconds to be the minimum amount for success. This article has been updated to reflect the latest data and images from the impact.
In a successful attempt to alter the orbit of an asteroid for the first time in history, NASA crashed a spacecraft into the asteroid Dimorphos on Sept. 26, 2022. The mission, known as the Double Asteroid Redirection Test, or DART, took place at an asteroid that posed no threat to our planet. Rather, it was an ideal target for NASA to test an important element of its planetary defense plan.
Read further to learn about DART, how it worked, and how the science and engineering behind the mission can be used to teach a variety of STEM topics.
Why It's Important
The vast majority of asteroids and comets are not dangerous, and never will be. Asteroids and comets are considered potentially hazardous objects, or PHOs, if they are 100-165 feet (30-50 meters) in diameter or larger and their orbit around the Sun comes within five million miles (eight million kilometers) of Earth’s orbit. NASA's planetary defense strategy involves detecting and tracking these objects using telescopes on the ground and in space. In fact, NASA’s Center for Near Earth Object Studies, or CNEOS, monitors all known near-Earth objects to assess any impact risk they may pose. Any relatively close approach is reported on the Asteroid Watch dashboard.

NASA's Planetary Defense Coordination Office runs a variety of programs and initiatives aimed at detecting and responding to threats from potentially hazardous objects, should one be discovered. The DART mission is one component and the first mission being flown by the team. Image credit: NASA | + Expand image
While there are no known objects currently posing a threat to Earth, scientists continue scanning the skies for unknown asteroids. NASA is actively researching and planning for ways to prevent or reduce the effects of a potential impact, should one be discovered. The DART mission was the first test of such a plan – in this case, whether it was possible to divert an asteroid from its predicted course by slamming into it with a spacecraft.
Eyes on Asteroids is a real-time visualization of every known asteroid or comet that is classified as a near-Earth object, or NEO. Asteroids are represented as blue dots and comets as shown as white dots. Use your mouse to explore the interactive further and learn more about the objects and how we track them. Credit: NASA/JPL-Caltech | Explore the full interactive
With the knowledge gained from the demonstration, similar techniques could be used in the future to deflect an asteroid or comet away from Earth if it were deemed hazardous to the planet.
How It Worked
With a diameter of about 525 feet (160 meters) – the length of 1.5 football fields – Dimorphos is the smaller of two asteroids in a double-asteroid system. Before DART's impact, Dimorphos orbited the larger asteroid called Didymos (Greek for "twin"), every 11 hours and 55 minutes.
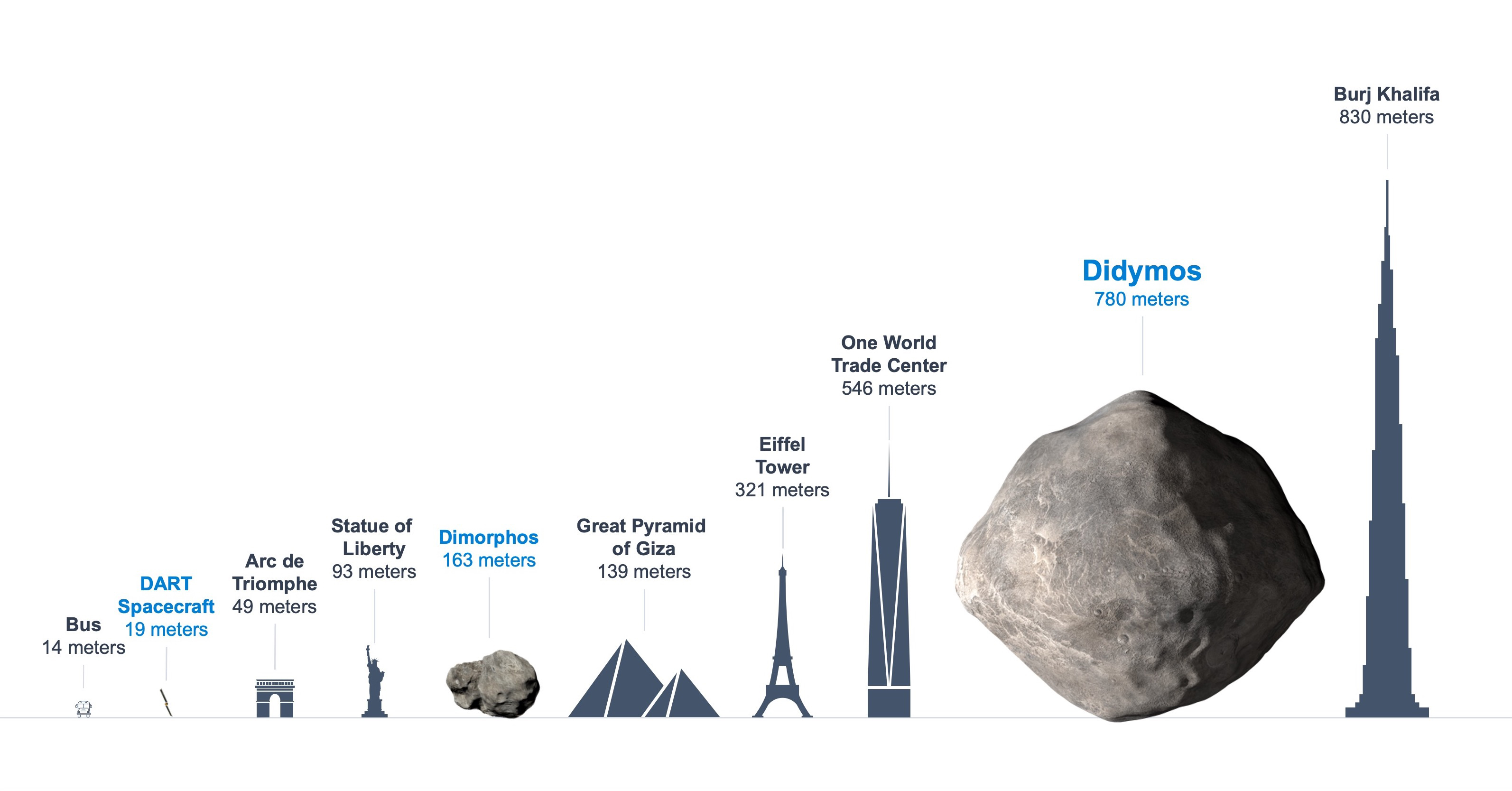
The sizes of the two asteroids in the Didymos system relative to objects on Earth. Image credit: NASA/Johns Hopkins APL | + Expand image
Neither asteroid poses a threat to our planet, which is one reason why this asteroid system was the ideal place to test asteroid redirection techniques. At the time of DART's impact, the asteroid pair was 6.8 million miles (11 million kilometers) away from Earth as they traveled on their orbit around the Sun.
The DART spacecraft was designed to collide head-on with Dimorphos to alter its orbit, shortening the time it takes the small asteroid to travel around Didymos. Compared with Dimorphos, which has a mass of about 11 billion pounds (five billion kilograms), the DART spacecraft was light. It weighed just 1,210 pounds (550 kilograms) at the time of impact. So how did such a light spacecraft affect the orbit of a relatively massive asteroid?
You can use your mouse to explore this interactive view of DART's impact with Dimorphos from NASA's Eyes on the Solar System. Credit: NASA/JPL-Caltech | Explore the full interactive
DART was designed as a kinetic impactor, meaning it transferred its momentum and kinetic energy to Dimorphos upon impact, altering the asteroid's orbit in return. Scientists were able to make predictions about some of these effects thanks to principles described in Newton's laws of motion.
Newton’s first law told us that the asteroid’s orbit would remain unchanged until something acted upon it. Using the formula for linear momentum (p = m * v), we could calculate that the spacecraft, which at the time of impact would be traveling at 3.8 miles (6.1 kilometers) per second, would have about 0.5% of the asteroid’s momentum. The momentum of the spacecraft may seem small in comparison, but calculations suggested it would be enough to make a detectable change in the speed of Dimorphos' orbit. However, mission planners felt that changing Dimorphos’ orbit by at least 73 seconds would be enough to consider the test a success.
But there was more to consider in testing whether the technique could be used in the future for planetary defense. For example, the formula for kinetic energy (KE = 0.5 * m * v2) tells us that a fast moving spacecraft possesses a lot of energy.
When DART hit the surface of the asteroid, its kinetic energy was 10 billion joules! A crater was formed and material known as ejecta was blasted out as a result of the impact. Scientists are still studying the data returned from the mission to determine the amount of material ejected out of the crater, but estimates prior to impact put the number at 10-100 times the mass of the spacecraft itself. The force needed to push this material out was then matched by an equal reaction force pushing on the asteroid in the opposite direction, as described by Newton’s third law.
This animation shows conceptually how DART's impact is predicted to change Dimorphos' orbit from a larger orbit to a slightly smaller one that's several minutes shorter than the original. Credit: NASA/Johns Hopkins APL/Jon Emmerich | Watch on YouTube
How much material was ejected and its recoil momentum is still unknown. A lot depends on the surface composition of the asteroid, which scientists are still investigating. Laboratory tests on Earth suggested that if the surface material was poorly conglomerated, or loosely formed, more material would be blasted out. A surface that was well conglomerated, or densely compacted, would eject less material.
After the DART impact, scientists used a technique called the transit method to see how much the impact changed Dimorphos' orbit. As observed from Earth, the Didymos pair is what’s known as an eclipsing binary, meaning Dimorphos passes in front of and behind Didymos from our view, creating what appears from Earth to be a subtle dip in the combined brightness of the pair. Scientists used ground-based telescopes to measure this change in brightness and calculate how quickly Dimorphos orbits Didymos. By comparing measurements from before and after impact, scientists determined that the orbit of Dimorphos had slowed by 32 minutes to 11 hours and 23 minutes.

The green circle shows the location of the Dimorphos asteroid, which orbits the larger asteroid, Didymos, seen here as the bright line across the middle of the images. The blue circle shows where Dimorphos would have been had its orbit not changed due to NASA’s DART mission purposefully impacting the smaller asteroid on Sept. 26, 2022. The images were obtained from the NASA Jet Propulsion Laboratory’s Goldstone planetary radar in California and the National Science Foundation’s Green Bank Observatory in West Virginia. Image credit: NASA/Johns Hopkins APL/JPL/NASA JPL Goldstone Planetary Radar/National Science Foundation’s Green Bank Observatory | + Expand image | › DART image gallery
One of the biggest challenges of the DART mission was navigating a small spacecraft to a head-on collision with a small asteroid millions of miles away. To solve that problem, the spacecraft was equipped with a single instrument, the DRACO camera, which worked together with an autonomous navigation system called SMART Nav to guide the spacecraft without direct control from engineers on Earth. About four hours before impact, images captured by the camera were sent to the spacecraft's navigation system, allowing it to identify which of the two asteroids was Dimorphos and independently navigate to the target.

A composite of 243 images of Didymos and Dimorphos taken by the DART spacecraft's DRACO camera on July 27, 2022, as the spacecraft was navigating to its target. Image credit: JPL DART Navigation Team | + Expand image | › DART image gallery
DART was not just an experimental asteroid impactor. The mission also used cutting-edge technology never before flown on a planetary spacecraft and tested new technologies designed to improve how we power and communicate with spacecraft.
Learn more about the engineering behind the DART mission, including the innovative Roll Out Solar Array and NEXT-C ion propulsion system, in this video featuring experts from the mission. Credit: APL | Watch on YouTube
One such technology that was first tested on the International Space Station and was later used on the solar-powered DART spacecraft, is the Roll Out Solar Array, or ROSA, power system. As its name suggests, the power system consisted of flexible solar panel material that was rolled up for launch and unrolled in space.

The Roll Out Solar Array, shown in this animated image captured during a test on the International Space Station, is making its first planetary journey on DART. Image credit: NASA | + Expand image
Some of the power generated by the solar array was used for another innovative technology, the spacecraft's NEXT-C ion propulsion system. Rather than using traditional chemical propulsion, DART was propelled by charged particles of xenon pushed from its engine. Ion propulsion has been used on other missions to asteroids and comets including Dawn and Deep Space 1, but DART's ion thrusters had higher performance and efficiency.
Follow Along
In the days following the event, NASA received images of the impact from a cubesat, LICIACube, that was deployed by DART before impact. The cubesat, which was provided by the Italian Space Agency, captured images of the impact and the ejecta cloud.

This image from LICIACube shows plumes of ejecta streaming from Dimorphos after DART's impact. Each rectangle represents a different level of contrast to better see fine structure in the plumes. By studying these streams of material, scientists will be able to learn more about the asteroid and the impact process. | + Expand image | › DART image gallery
Meanwhile, the James Webb Space Telescope, the Hubble Space Telescope, and the Lucy spacecraft observed Didymos to monitor how soon reflected sunlight from the ejecta plume could be seen. Going forward, DART team members will continue observing the asteroid system to measure the change in Dimorphos’ orbit and determine what happened on its surface. And in 2024, the European Space Agency plans to launch the Hera spacecraft to conduct an in-depth post-impact study of the Didymos system.

This animation, a timelapse of images from NASA’s James Webb Space Telescope, covers the time spanning just before DART's impact at 4:14 p.m. PDT (7:14 p.m. EDT) on Septtember 26 through 5 hours post-impact. Plumes of material from a compact core appear as wisps streaming away from where the impact took place. An area of rapid, extreme brightening is also visible in the animation. Image credit: Science: NASA, ESA, CSA, Cristina Thomas (Northern Arizona University), Ian Wong (NASA-GSFC); Joseph DePasquale (STScI) | + Expand image | › DART image gallery
Continue following along with all the science from DART, including the latest images and updates on the mission website. Plus, explore even more resources on this handy page.
Teach It
The mission is a great opportunity to engage students in the real world applications of STEM topics. Start exploring these lessons and resources to get students engaging in STEM along with the mission.
Educator Guides
Expert Talks
Student Activities
Articles
-
 Teachable Moments
Teachable MomentsHow NASA Studies and Tracks Asteroids Near and Far
Here’s how NASA uses math and science to track the movements of asteroids and find out what they’re made of – and students can, too.
-
 Meet JPL Interns
Meet JPL InternsFrom Island Life to Spotting Asteroids for NASA
Meet a JPL intern whose journey took her from the remote island of Saipan to a team helping track asteroids at NASA.
Resources for Kids
Check out these related resources for kids from NASA Space Place:
- Article for Kids: Asteroid or Meteor: What's the Difference?
- Article for Kids: What Is an Asteroid?
- Article for Kids: Why Does the Moon Have Craters?
- Article for Kids: What Is an Impact Crater?
Explore More
- Facts & Figures: Didymos In Depth
- Facts & Figures: DART Mission
- Website: DART Mission
- Gallery: DART Mission Images and Videos
- Facts & Figures: Asteroid Watch
- Gallery: Next Five Asteroid Approaches
- Articles: Asteroid News and Images from JPL
- Eyes on Asteroids
- Eyes on the Solar System - DART Impact
- Quiz: Are You a Planetary Defnder?
- Center for Near-Earth Object Studies
TAGS: Asteroids and Comets, DART, near-Earth objects, planetary defense, Science, K-12 Education, Teachers, Educators, Parents, Teachable Moments, Asteroid TM
Teachable Moments | October 4, 2022
How to Watch a Total Lunar Eclipse and Get Students Observing the Moon
There’s no better time to learn about the Moon than during a lunar eclipse. Here’s how eclipses work, what to expect, and how to get students engaged.
This article has been updated to include information about the visibility and timing of the total lunar eclipse on Nov. 8, 2022. See What to Expect for details.
A full moon is always a good reason to go outside and look up, but a total or partial lunar eclipse is an awe-inspiring site that gives students a great opportunity to engage in practical sky watching. Whether it’s the Moon's reddish hue during a total lunar eclipse or the "bite" taken out of the Moon during a partial lunar eclipse, there's always something exciting to observe during these celestial events.
Read on to see what to expect during the next lunar eclipse. Plus, explore resources you can use at home or in the classroom to teach students about moon phases, craters, and more!
How It Works

These side-by-side graphics show how the Moon, Sun, and Earth align during a lunar eclipse (left) versus a non-eclipse full moon (right). Credit: NASA Goddard Visualization Studio | + Enlarge image
Eclipses can occur when the Sun, the Moon and Earth align. Lunar eclipses can only happen during the full moon phase, when the Moon and the Sun are on opposite sides of Earth. At that point, the Moon could move into the shadow cast by Earth, resulting in a lunar eclipse. However, most of the time, the Moon’s slightly tilted orbit brings it above or below the shadow of Earth.
The time period when the Moon, Earth and the Sun are lined up and on the same plane – allowing for the Moon to pass through Earth’s shadow – is called an eclipse season. Eclipse seasons last about 34 days and occur just shy of every six months. When a full moon occurs during an eclipse season, the Moon travels through Earth’s shadow, creating a lunar eclipse.
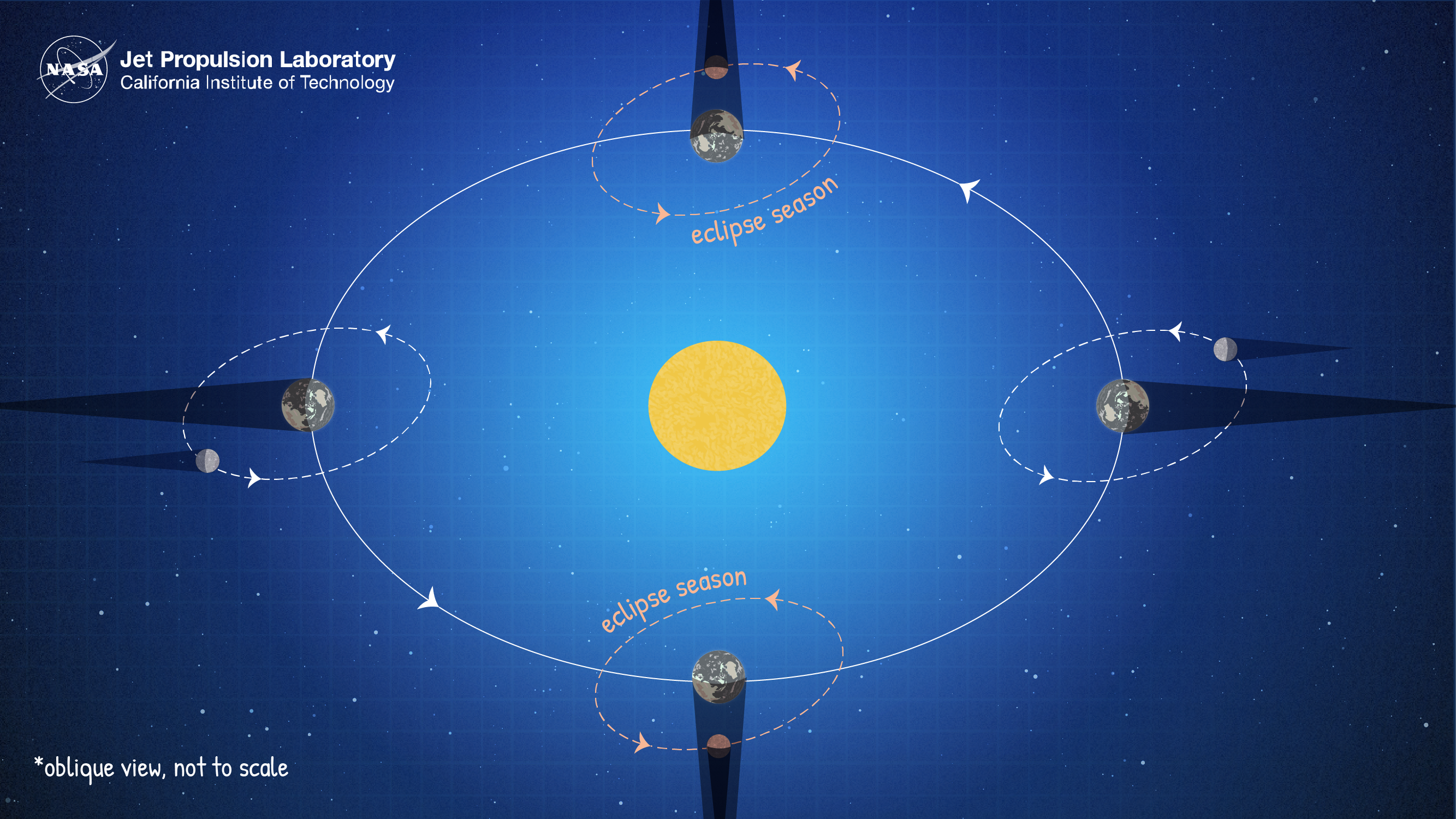
When a full moon occurs during an eclipse season, the Moon travels through Earth's shadow, creating a lunar eclipse. Credit: NASA/JPL-Caltech | + Enlarge image
Unlike solar eclipses, which require special glasses to view and can only be seen for a few short minutes in a very limited area, a total lunar eclipse can last over an hour and be seen by anyone on the nighttime side of Earth – as long as skies are clear!
Why It’s Important
Lunar eclipses have long played an important role in understanding Earth and its motions in space.
In ancient Greece, Aristotle noted that the shadows on the Moon during lunar eclipses were round, regardless of where an observer saw them. He realized that only if Earth were a spheroid would its shadows be round – a revelation that he and others had many centuries before the first ships sailed around the world.
Earth wobbles on its axis like a spinning top that’s about to fall over, a phenomenon called precession. Earth completes one wobble, or precession cycle, over the course of 26,000 years. Greek astronomer Hipparchus made this discovery by comparing the position of stars relative to the Sun during a lunar eclipse to those recorded hundreds of years earlier. A lunar eclipse allowed him to see the stars and know exactly where the Sun was for comparison – directly opposite the Moon. If Earth didn’t wobble, the stars would appear to be in the same place they were hundreds of years earlier. When Hipparchus saw that the stars’ positions had indeed moved, he knew that Earth must wobble on its axis!
Additionally, modern-day astronomers have used ancient eclipse records and compared them with computer simulations. These comparisons helped scientists determine the rate at which Earth’s rotation is slowing.
What to Expect
The Moon passes through two distinct parts of Earth’s shadow during a lunar eclipse. The outer part of the cone-shaped shadow is called the penumbra. The penumbra is less dark than the inner part of the shadow because it’s penetrated by some sunlight. (You have probably noticed that some shadows on the ground are darker than others, depending on how much outside light enters the shadow; the same is true for the outer part of Earth’s shadow). The inner part of the shadow, known as the umbra, is much darker because Earth blocks additional sunlight from entering the umbra.
Here's what to expect during the total lunar eclipse on Nov. 8, 2022, which will be visible in North and South America, as well as Asia and Australia. Viewers in the most eastern parts of the continental U.S. will see the Moon set below the horizon as it exits Earth’s shadow in the second half of the eclipse.
At 12:02 a.m. PST (3:02 a.m. EST), the edge of the Moon will begin entering the penumbra. The Moon will dim very slightly for the next 67 minutes as it moves deeper into the penumbra. Because this part of Earth’s shadow is not fully dark, you may only notice some dim shading (if anything at all) on the Moon near the end of this part of the eclipse. Should you decide to skip this part of the eclipse, you won’t miss much.

During a total lunar eclipse, the Moon first enters into the penumbra, or the outer part of Earth's shadow, where the shadow is still penetrated by some sunlight. Credit: NASA | + Enlarge image
At 1:09 a.m. PST (4:09 a.m. EST), the edge of the Moon will begin entering the umbra. As the Moon moves into the darker shadow, significant darkening will be noticeable. Some say that during this part of the eclipse, the Moon looks as if it has had a bite taken out of it. That “bite” gets bigger and bigger as the Moon moves deeper into the shadow.

As the Moon starts to enter into the umbra, the inner and darker part of Earth's shadow, it appears as if a bite has been taken out of the Moon. This "bite" will grow until the Moon has entered fully into the umbra. Credit: NASA | + Enlarge image
At 2:16 a.m. PST (5:16 a.m. EST), the Moon will be completely inside the umbra, marking the beginning of the total lunar eclipse, also known as totality.
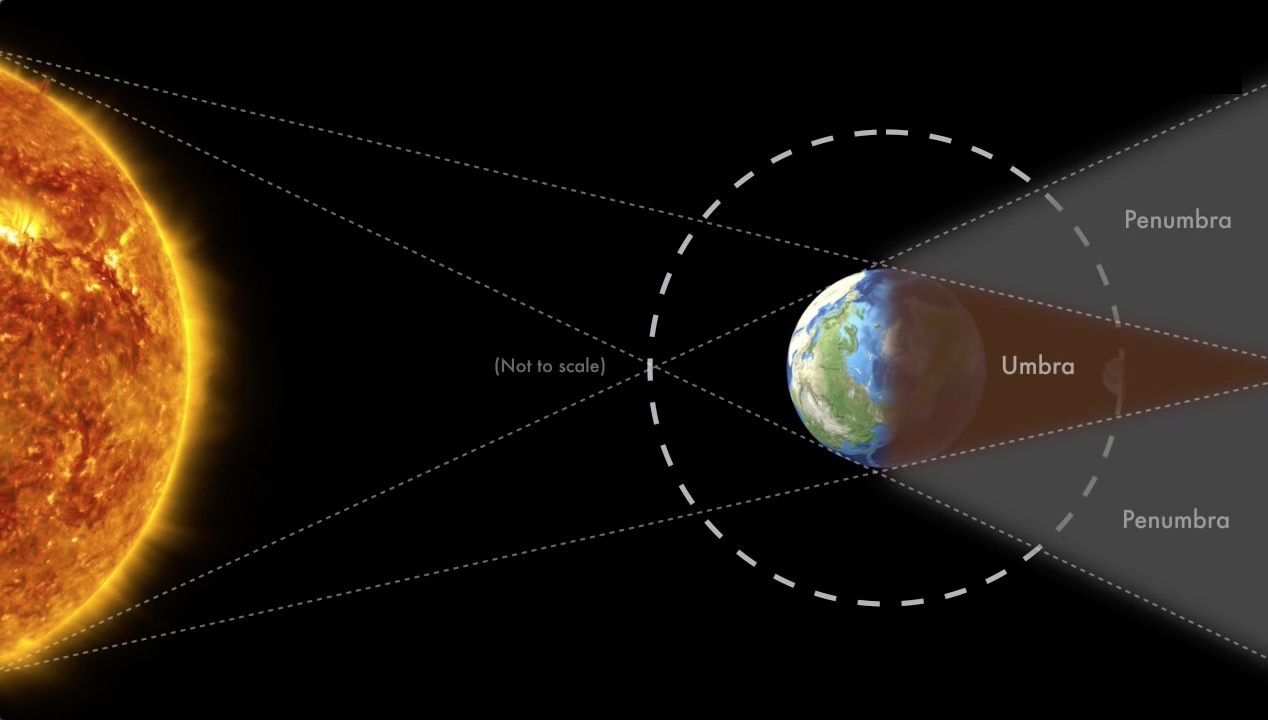
The total lunar eclipse starts once the moon is completely inside the umbra. And the moment of greatest eclipse happens with the Moon is halfway through the umbra as shown in this graphic. Credit: NASA | + Enlarge image
The moment of greatest eclipse, when the Moon is halfway through its path across the umbra, occurs at 2:59 a.m. PST (5:59 a.m. EST). As the Moon moves completely into the umbra – the part of the eclipse known as totality – something interesting happens: The Moon begins to turn reddish-orange. The reason for this phenomenon? Earth’s atmosphere. As sunlight passes through it, the small molecules that make up our atmosphere scatter blue light, which is why the sky appears blue. This leaves behind mostly red light that bends, or refracts, into Earth’s shadow. We can see the red light during an eclipse as it falls onto the Moon in Earth’s shadow. This same effect is what gives sunrises and sunsets a reddish-orange color.

As the Moon moves completely into the umbra, it turns a reddish-orange color. Credit: NASA | + Enlarge image
A variety of factors affect the appearance of the Moon during a total lunar eclipse. Clouds, dust, ash, photochemical droplets and organic material in the atmosphere can change how much light is refracted into the umbra. The potential for variation provides a great opportunity for students to observe and classify the lunar eclipse based on its brightness. Details can be found below in the Teach It section.
At 3:41 a.m. PST (6:41 a.m. EST), the edge of the Moon will begin exiting the umbra and moving into the opposite side of the penumbra, reversing the “bite” pattern seen earlier. At this point, the Moon will have just set in the most northeastern portions of the continental United States. More and more eastern states will see the Moon set over the next hour as the eclipse progresses.
At 4:49 a.m. PST, the Moon will be completely outside of the umbra and no longer visible in the eastern United States. Those in the central United States will see the Moon begin setting around this time (6:49 a.m. CST). The Moon will continue exiting the penumbra until the eclipse officially ends at 5:56 a.m. PST, remaining visible only to viewers in the western United States, including many in the Mountain Time Zone one hour ahead.
Teach It
Ask students to observe the lunar eclipse and evaluate the Moon’s brightness using the Danjon Scale of Lunar Eclipse Brightness. The Danjon scale illustrates the range of colors and brightness the Moon can take on during a total lunar eclipse and is a tool observers can use to characterize the appearance of an eclipse. View the lesson guide here. After the eclipse, have students compare and justify their evaluations of the eclipse.
Use these standards-aligned lessons and related activities to get your students excited about the eclipse, moon phases, and Moon observations.
Educator Guides & Resources
-

Evaluating a Lunar Eclipse
Students use the Danjon Scale of Lunar Eclipse Brightness to illustrate the range of colors and brightness the Moon can take on during a total lunar eclipse.
Grades 3-12
Time 30 mins - 1 hr
-

When Do Lunar Eclipses Happen?
Students use a paper plate to make a model that explains why lunar eclipses don’t occur during every full moon.
Grades 4-8
Time Less than 30 mins
-

Observing the Moon
Students identify the Moon’s location in the sky and record their observations over the course of the moon-phase cycle in a journal.
Grades K-6
Time 30 mins - 1 hr
-

Moon Phases
Students learn about the phases of the moon by acting them out.
Grades 1-6
Time 30 mins - 1 hr
-

Whip Up a Moon-Like Crater
Whip up a moon-like crater with baking ingredients as a demonstration for students.
Grades 1-6
Time 30 mins - 1 hr
-

Modeling the Earth-Moon System
Students learn about scale models and distance by creating a classroom-size Earth-Moon system.
Grades 6-8
Time 30 mins - 1 hr
-

All Moon Lessons for Educators
Teach students all about the Moon with these standards-aligned STEM lessons for educators.
Grades K-12
Time Varies
Student Activities
-

When Do Lunar Eclipses Happen?
Use a paper plate to make a model that explains why lunar eclipses don’t happen as often as you might expect.
-

Make a Moon Phases Calendar and Calculator
Like a decoder wheel for the Moon, this calendar will show you where and when to see the Moon and every moon phase throughout the year!
-

Look at the Moon! Journaling Project
Draw what you see in a Moon Journal and see if you can predict the moon phase that comes next.
-

Make a Moon Crater
Make craters like the ones you can see on the Moon using simple baking ingredients!
-

All Moon Activities for Students
Make a moon phases calendar, moon crater, lunar rover and more with these activities all about Earth's moon.
Subjects Varies
Type Varies
Explore More
- Try these related resources for students from NASA's Space Place:
- Article for Kids: Lunar Eclipses and Solar Eclipses
- Article for Kids: Why Does the Moon Have Craters?
- Article for Kids: All About the Moon
- NASA Moon Website – Find out more about the Moon and the NASA robots and humans who have visited it.
TAGS: Lunar Eclipse, Moon, Super Blue Blood Moon, Observe the Moon, Eclipse, K-12, Classroom Activities, Teaching





















