Lesson .
.Pi in the Sky 7
Overview
In the seventh installment of the "Pi in the Sky" illustrated problem set, students use the mathematical constant pi to solve real-world science and engineering problems. Students will use pi to compare the sizes of Mars landing areas, calculate the length of a year for one of the most distant objects in the solar system, measure the depth of the ocean from an airplane, and determine the diameter of a distant debris disk.
Materials
- Pi in the Sky 7 poster – Download PDF
- Pi in the Sky 7 handouts – Download PDF
- Pi in the Sky 7 answer key – Download PDF
- Pi in the Sky 7 answer handouts – Download PDF (also available as a text-only doc)
- "Pi in the Sky" series slideshow (mobile, tablet and screen-reader friendly)
Background
Mars Maneuver
Long before a Mars rover touches down on the Red Planet, scientists and engineers must determine where to land. Rather than choosing a specific landing spot, NASA selects an area known as a landing ellipse. A Mars rover could land anywhere within this ellipse. Choosing where the landing ellipse is located requires compromising between getting as close as possible to interesting science targets and avoiding hazards like steep slopes and large boulders, which could quickly bring a mission to its end. In the Mars Maneuver problem, students use pi to see how new technologies have reduced the size of landing ellipses from one Mars rover mission to the next.
Cold Case
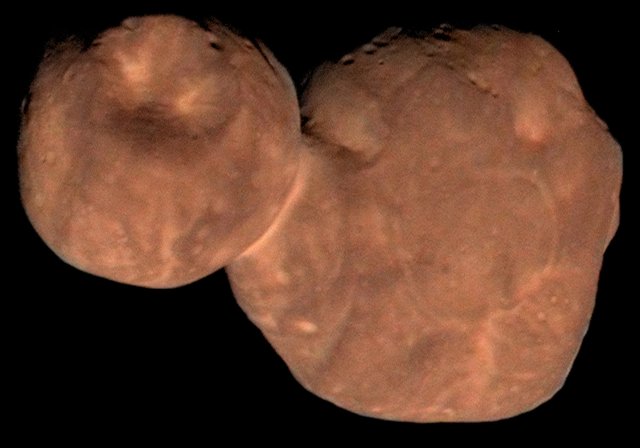
In January 2019, NASA's New Horizons spacecraft sped past Arrokoth, a frigid, primitive object that orbits within the Kuiper Belt, a doughnut-shaped ring of icy bodies beyond the orbit of Neptune. Arrokoth is the most distant Kuiper Belt object to be visited by a spacecraft and only the second object in the region to have been explored up close. To get New Horizons to Arrokoth, mission navigators needed to know the orbital properties of the object, such as its speed, distance from the Sun, and the tilt and shape of its orbit. This information is also important for scientists studying the object. In the Cold Case problem, students can use pi to determine how long it takes the distant object to make one trip around the Sun.
Coral Calculus
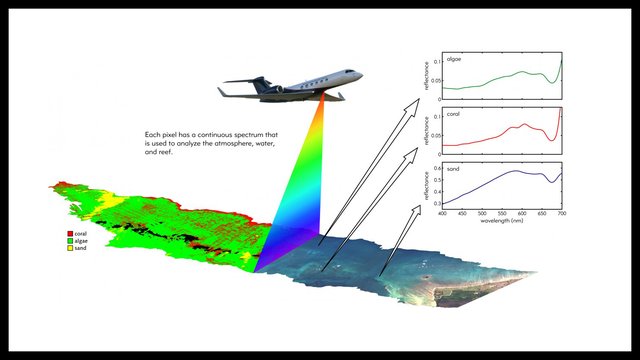
Coral reefs provide food and shelter to many ocean species and protect coastal communities against extreme weather events. Ocean warming, invasive species, pollutants, and acidification caused by climate change can harm the tiny living coral organisms responsible for building coral reefs. To better understand the health of Earth's coral reefs, NASA's COral Reef Airborne Laboratory, or CORAL, mission maps them from the air using spectroscopy, studying how light interacts with the reefs. To make accurate maps, CORAL must be able to differentiate among coral, algae and sand on the ocean floor from an airplane. And to do that, it needs to calculate the depth of the ocean at every point it maps by measuring how much sunlight passes through the ocean and is reflected upward from the ocean floor. In Coral Calculus, students use pi to measure the water depth of an area mapped by the CORAL mission and help scientists better understand the status of Earth's coral reefs.
Planet Pinpointer
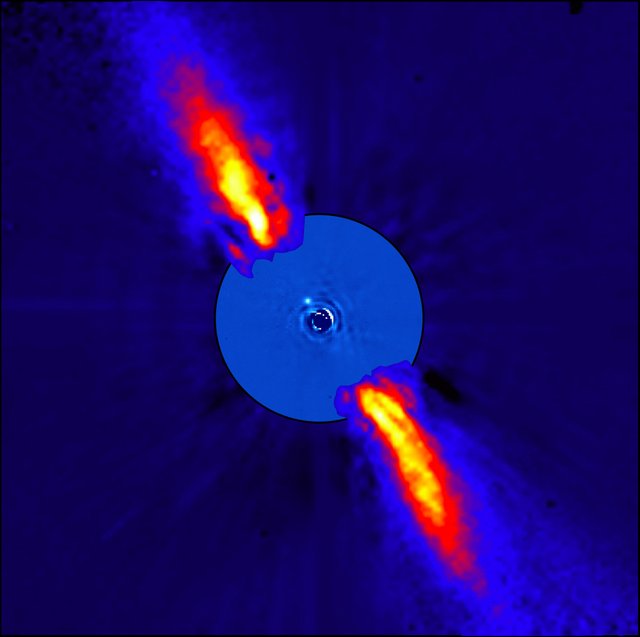
Our galaxy contains billions of stars, many of which are likely home to exoplanets – planets outside our solar system. So how do scientists decide where to look for these worlds? Using data gathered by NASA's Spitzer Space Telescope, researchers found that they're more likely to find giant exoplanets around young stars surrounded by debris disks, which are made up of material similar to what's found in the asteroid belt and Kuiper Belt in our solar system. Sure enough, after discovering a debris disk around the star Beta Pictoris, researchers later confirmed that it is home to at least two giant exoplanets. Learning more about Beta Pictoris' debris disk could give scientists insight into the formation of these giant worlds. In Planet Pinpointer, put yourself in the role of a NASA scientist to learn more about Beta Pictoris' debris disk, using pi to calculate the distance across it.
Procedures
Mars Maneuver
When we plan where to land a spacecraft on Mars, we don’t choose a specific spot, but a larger area called a landing ellipse. It's like choosing a parking lot rather than a parking spot. To choose a landing ellipse, we have to compromise between getting as close as possible to interesting science targets and avoiding hazards. As we've created new technology to help direct spacecraft, landing ellipses have gotten smaller and smaller. That means that we're able to land in places we couldn't before and get closer to the stuff we want to study.
In 2012, the Curiosity rover used its sky crane landing system to touch down in a 20 km by 7 km ellipse. When the Perseverance rover lands on Feb. 18, 2021, it will use the same system along with a new technique called Range Trigger that will allow the spacecraft to land in the smallest ellipse yet, measuring just 13 km by 7 km. What percentage of Curiosity's landing ellipse is Perseverance's landing ellipse?
Cold Case
In January 2019, NASA's New Horizons spacecraft flew within 3,538 km of the most distant and primitive object explored up-close by a spacecraft. The object was originally known as 2014 MU69, but it was later renamed Arrokoth. It looks like a partially flattened, reddish snowman and is made up of two objects that merged into one. Found 6.6 billion km from Earth, Arrokoth is a small “Cold Classical” Kuiper Belt object, meaning it orbits the Sun in a nearly circular path and has a low orbital inclination. Cold Classical objects make up about one-third of the Kuiper Belt.
One reason scientists are interested in studying Arrokoth and other Kuiper Belt objects is that they are thought to be well preserved, frozen samples of what the outer solar system was like at its birth, more than 4.5 billion years ago. Learn a bit more about Arrokoth by calculating how long it takes the object to make one trip around the Sun.
Coral Calculus
Flying aboard an aircraft, NASA’s CORAL mission uses spectroscopy to study the health of coral reefs and the threats they face. To differentiate among coral, algae and sand on the ocean floor, CORAL computes the depth of every point it maps. The water’s depth can be determined using the “absorption coefficient,” indicating how much light is absorbed through a given depth of water.
Imagine CORAL collects a light measurement reflected by white sand covered by an unknown depth of water that is 76% in the blue and 4.5% in the red. Using the formulas below, calculate the water’s depth. Note that sunlight passes through the water twice: when traveling from the Sun to the ocean floor and when reflecting up to the aircraft.
absorption coefficient, α = (4πk)/λ k = coefficient of the imaginary number portion of the refractive index λ = wavelength (meters) of light observed
Beer-Lambert law, T = e(-α•d) T = observed reflectance, or transmittance (T), of light through a distance (d) of water
Refractive Indices:
- Water in the blue wavelength (450 nm) = 1.3369 + 1.01E-09i
- Water in the red wavelength (650 nm) = 1.3314 + 1.60E-08i
Planet Pinpointer
Our galaxy contains billions of stars, most of which are likely home to exoplanets – planets outside our solar system. How do scientists decide where to look for these worlds? Researchers looking at data from NASA's Spitzer Space Telescope found that giant exoplanets tend to exist around young stars surrounded by a disk of debris. A prominent debris disk around the star Beta Pictoris, which is 6 x 1014 km away from Earth, lead scientists to discover two exoplanets several times bigger than Jupiter orbiting the star! Learning more about the debris disk could give scientists insight into the formation of these giant worlds.
Given the angle of the disk's apparent size is 169 arcseconds, determine the actual distance across it using the formula for small angle approximation, below. (An arcsecond is 1/3,600 of a degree.)
D = dθ D = distance across the debris disk (km) d = distance to Beta Pictoris (km) θ = angle of apparent size (radians)
Assessment
Extensions
Participate
Join the conversation and share your Pi Day Challenge answers with @NASAJPL_Edu on social media using the hashtag #NASAPiDayChallenge
